题目内容
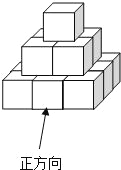
【题目】把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色![]() 不含底面
不含底面![]()
![]() 该几何体中有多少小正方体?
该几何体中有多少小正方体?
![]() 画出主视图.
画出主视图.
![]() 求出涂上颜色部分的总面积.
求出涂上颜色部分的总面积.
【答案】(1)14个;(2)见解析;(3)33cm2
【解析】试题分析:(1)该几何体中正方体的个数为最底层的9个,加上第二层的4个,再加上第三层的1个;
(2)主视图从上往下三行正方形的个数依次为1,2,3;
(3)涂上颜色部分的总面积可分上面,前面,后面,左面,右面,相加即可.
试题解析:(1)该几何体中正方体的个数为9+4+1=14个;
(2)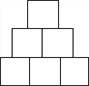 ;
;
(3)先算侧面﹣﹣底层12个小面 中层8个 上层4个再算上面﹣﹣上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9﹣4)=5个总共33个小面.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目