Question

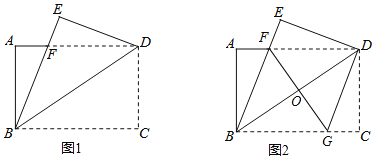
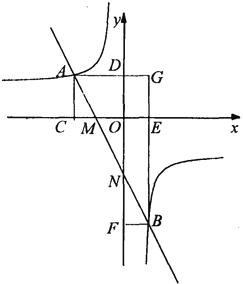
【题目】已知：如图，AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F，连接CF.

(1)如图1，求证：四边形ADCF是平行四边形；

(2)如图2，连接CE,在不添加任何辅助线的情况下,请直接写出图2中所有与△BDE面积相等的三角形.

Answer 1

【答案】(1)证明见解析；(2)△AEF、 △ABE、 △ACE 、△CDE.

【解析】

(1)证明△AEF≌△DEB，可得AF=DB，再根据 BD=CD可得AF=CD，再由AF//CD，根据有一组对边平行且相等的四边形是平行四边形即可证得结论；

(2)根据三角形中线将三角形分成面积相等的两个三角形以及全等三角形的面积相等即可得.

(1)D为BC的点、E为AD的中点

BD=CD、AE=DE

AF∥BC，

∴∠AFE=∠DBE，

在△AEF和△DEB中

，

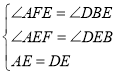∴△AEF≌△DEB，

∴AF=DB，

又∵ BD=CD

∴AF=CD，

又AF∥BC，

∴四边形ADCF是平行四边形；

(2)∵△AEF≌△DEB，

∴S△AEF=S△DEB，

∵D为BC中点，

∴S△CDE=S△DEB，

∵E为AD中点，

∴S△ABE=S△DEB，S△ACE= S△CDE=S△DEB，

综上，与△BDE面积相等的三角形有△AEF、 △ABE、 △ACE 、△CDE.