Question

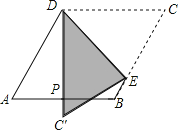
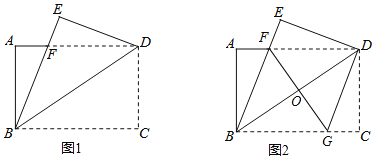
【题目】如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．

（1）求证：△BDF是等腰三角形；

（2）如图2，过点D作DG∥BE，交BC于点G，连接FG交BD于点O．

①判断四边形BFDG的形状，并说明理由；

②若AB=6，AD=8，求FG的长为 ．

Answer 1

【答案】（1）见解析；（2）①四边形BFDG是菱形．理由见解析；②FG=．

【解析】

（1）证明△BDF是等腰三角形，可证明BF=DF，可通过证明∠EBD=∠FDB实现，利用折叠的性质和平行线的性质解决．

（2）①先判断四边形BFDG是平行四边形，再由（1）BF=FD得到结论；②要求FG的长，可先求出OF的长，在Rt△BFO中，BO可由AB、AD的长及菱形的性质求得，解决问题的关键是求出BF的长．在Rt△BFA中，知AB=6、AF+BF=AD=8，可求出BF的长，问题得以解决．

（1）∵四边形ABCD是矩形，

∴AD∥BC，

∴∠ADB=∠CBD，

由折叠的性质可知：∠EBD=∠CBD，

∴ADB=∠EBD，

∴BF=FD

∴△BDF是等腰三角形

（2）①四边形BFDG是菱形．

理由：∵FD∥BG，DG∥BE，

∴四边形BFDG是平行四边形

又∵BF=DF，

∴四边形BFDG是菱形

②设AF=x，则FD=8-x，

∴BF=FD=8-x

在Rt△ABF中，

62+x2=（8-x）2，

解得：x=，

∴FD=8-=，

在Rt△ABD中，∵AB=6，AD=8，

∴BD=10

∵四边形BFDG是菱形，

∴OD=BD=5，FO=FG，FG⊥BD，

在Rt△ODF中，

∵FO2+DO2=FD2，即FO2+52=（）2，

∴FO=，

∴FG=2FO=．

故答案为：．