Question

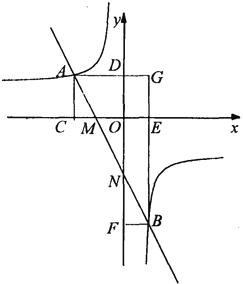
【题目】直线MN与x轴、y轴分别交于点M、N，并且经过第二、三、四象限，与反比例函数y＝（k＜0）的图象交于点A、B，过A、B两点分别向x轴、y轴作垂线，垂足为C、D、E、F，AD与BF交于G点．

（1）比较大小：S矩形ACOD　 S矩形BEOF（填“＞，＝，＜”）．

（2）求证：①AGGE＝BFBG；

②AM＝BN；

（3）若直线AB的解析式为y＝﹣2x﹣2，且AB＝3MN，则k的值为　 ．

Answer 1

【答案】（1）＝；（2）①见解析，②见解析；（3）﹣4．

【解析】

(1)根据反比例函数的比例系数的几何意义即可作出判断；

(2)①设A的横坐标是a，B的横坐标是b，分别代入y＝，则A的坐标是(a，)，B的坐标是(b，)，利用a、b表示出AG、GE、BF、BG的长，即可证得；

②求得直线AB的解析式，即可求得M的坐标，即可证明CM＝BF，即可证得△ACM≌△NFB，根据全等三角形的对应边相等，即可证得；

(3)根据AM＝BN，且AB＝3MN，可以得到AM＝BN＝MN，则OF＝2ON，OM＝BF，在y＝﹣2x﹣2中，求得M、N的坐标，即可求得B的坐标，代入反比例函数解析式即可求得k的值．

(1)根据反比例函数k的几何意义可得：S矩形ACOD＝S矩形BEOF＝|k|，

故答案为：＝；

(2)①设A的横坐标是a，B的横坐标是b，分别代入y＝，则A的坐标是(a，)，B的坐标是(b，)，

则AG＝b﹣a，GE＝，BF＝b，BG＝﹣，

则AGGE＝(b﹣a)＝，

BFBG＝b(﹣)＝，

∴AGGE＝BFBG；

②设过A、B的直线的解析式是y＝mx+n，则，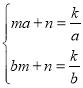

解得：，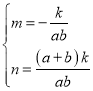

则函数的解析式是：y＝﹣x+，

令y＝0，解得：x＝a+b，

则M的横坐标是a+b，

∴CM＝a+b﹣a＝b，

∴CM＝BF，

则△ACM≌△NFB，

∴AM＝BN；

(3)∵AM＝BN，且AB＝3MN，

∴AM＝BN＝MN，

∴ON＝NF，

在y＝﹣2x﹣2中，令x＝0，解得：y＝﹣2，

则ON＝2，

令y＝0，解得：x＝﹣1，则OM＝1，

∴OF＝2ON＝4，OM＝BF＝1

∴B的坐标是(1，﹣4)，

把(1，﹣4)代入y＝中，得：k＝﹣4，

故答案为：﹣4．