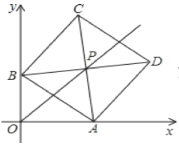
[题目]如图.正方形网格中的每个小正方形的边长都是1.每个小格的顶点叫格点.网格中有以格点A.B.C为顶点的△ABC.请你根据所学的知识回答下列问题:(1)求△ABC的面积,(2)判断△ABC的形状.并说明理由．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫格点，网格中有以格点A、B、C为顶点的△ABC，请你根据所学的知识回答下列问题：

（1）求△ABC的面积；（2）判断△ABC的形状，并说明理由．

【答案】（1）△ABC 的面积为5；（2）△ABC是直角三角形，见解析.

【解析】

(1)三角形ABC面积由长方形面积减去三个直角三角形面积，求出即可；

(2)利用勾股定理表示出AB2=5，BC2=25，AC2=20，再利用勾股定理的逆定理得到三角形为直角三角形．

(1 )S△ABC =4 ×4-×1×2 -×4 ×3- ×2×4 =16-1-6-4＝5；

(2)△ABC是直角三角形，理由：

∵正方形小方格边长为1

∴AB2＝12+22＝5，AC2＝22+42＝20，BC2＝32+42＝25，

∴AB2+ AC2= BC2，

∴△ABC是直角三角形.

练习册系列答案

（1）如图2所示，一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动5个单位长度，可以看到终点表示的数是﹣2，利用数形结合思想，请参照下图并思考，完成下列各题：

①数轴上表示2与﹣5的两点之间的距离是　　个单位长度．

②若数轴上的点A表示的数为x，点B表示的数为﹣1，则A与B两点的距离可以表示为　　；若|x+1|=3，则x为　　．

③如果点A表示数﹣1，将A点向右移动18个单位长度，再向左移动13个单位长度终点为B，那么A，B两点间的距离是　　．

（2）若数轴上的点A表示的数为x且x为整数，则当x为　　时，|x+5|与|x﹣7|的值相等．

【题目】根据爱因斯坦的相对论可知，任何物体的运动速度不能超过光速（3×105km/s），因为一个物体达到光速需要无穷多的能量，并且时光会倒流，这在现实中是不可能的．但我们可让一个虚拟物超光速运动，例如：直线l，m表示两条木棒相交成的锐角的度数为10°，它们分别以与自身垂直的方向向两侧平移时，它们的交点A也随着移动（如图箭头所示），如果两条直线的移动速度都是光速的0.2倍，则交点A的移动速度是光速的_____倍．（结果保留两个有效数字）．

【题目】在平面直角坐标系xOy中,边长为5的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O)，顶点C. D都在第一象限。

(1)当点A坐标为(4,0)时，求点D的坐标；

(2)求证：OP平分∠AOB；

(3)直接写出OP长的取值范围(不要证明).

【题目】市首批一次性投放公共自行车700辆供市民租用出行，由于投入数量不够，导致出现需要租用却未租到车的现象，现随机抽取的某五天在同一时段的调查数据汇成如下表格.

请回答下列问题:

时间	第一天7：00﹣8：00	第二天7：00﹣8：00	第三天7：00﹣8：00	第四天7：00﹣8：00	第五天7：00﹣8：00
需要租用自行车却未租到车的人数（人）	1500	1200	1300	1300	1200

（1）表格中的五个数据（人数）的中位数是多少？

（2）由随机抽样估计，平均每天在7:00-8:00 :需要租用公共自行车的人数是多少？

【题目】如图，抛物线y=ax2+bx经过点A（﹣1，）及原点，交x轴于另一点C（2，0），点D（0，m）是y轴正半轴上一动点，直线AD交抛物线于另一点B．

（1）求抛物线的解析式；

（2）如图1，连接AO、BO，若△OAB的面积为5，求m的值；

（3）如图2，作BE⊥x轴于E，连接AC、DE，当D点运动变化时，AC、DE的位置关系是否变化？请证明你的结论．

【题目】阅读下列材料，完成任务：

自相似图形

定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．

任务：

（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为　　；

（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为　　；

（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．

请从下列A、B两题中任选一条作答：我选择　　题．

A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=　　（用含b的式子表示）；

②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=　　（用含n，b的式子表示）；

B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=　　（用含b的式子表示）；

②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=　　（用含m，n，b的式子表示）．

【题目】定义运算ab＝a(1－b)，下面给出了关于这种运算的四个结论：

①2(－2)＝6 ②ab＝ba

③若a＋b＝0，则(aa)＋(bb)＝2ab ④若ab＝0，则a＝0．

其中正确结论的序号是 (填上你认为所有正确结论的序号)．

【题目】已知：如图，AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F，连接CF.

(1)如图1，求证：四边形ADCF是平行四边形；

(2)如图2，连接CE,在不添加任何辅助线的情况下,请直接写出图2中所有与△BDE面积相等的三角形.

试题分类