题目内容
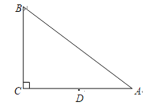
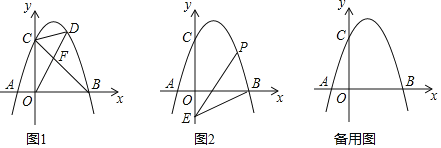
【题目】如图所示,为测量河岸两灯塔![]() ,
,![]() 之间的距离,小明在河对岸
之间的距离,小明在河对岸![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,灯塔
方向上,灯塔![]() 在东北方向上,小明沿河岸向东行走100米至
在东北方向上,小明沿河岸向东行走100米至![]() 处,测得此时灯塔
处,测得此时灯塔![]() 在北偏西
在北偏西![]() 方向上,已知河两岸
方向上,已知河两岸![]() .
.
(1)求观测点![]() 到灯塔
到灯塔![]() 的距离;
的距离;
(2)求灯塔![]() ,
,![]() 之间的距离.
之间的距离.
【答案】(1)![]() (米);(2)
(米);(2)![]() (米)
(米)
【解析】
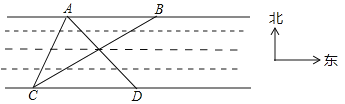
(1)过点C作CM⊥AD于M,过点A作AN⊥BC于N,由题意易知,在△CDM中,∠MCD=30°,得出DM=![]() CD=50米,CM=50
CD=50米,CM=50![]() 米,Rt△ACM中,由∠CAM=45°,得出AM=CM=50
米,Rt△ACM中,由∠CAM=45°,得出AM=CM=50![]() 米,从而得到AC的长;
米,从而得到AC的长;
(2)在Rt△ACN中,∠ACN=45°-15°=30°,得出AN=![]() AC=25
AC=25![]() 米,在Rt△ABN中,∠ABC=∠BCD=45°,由等腰直角三角形的性质即可得出答案.
米,在Rt△ABN中,∠ABC=∠BCD=45°,由等腰直角三角形的性质即可得出答案.
解:(1)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
由题意可知![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() (米),
(米),![]() 米,
米,
又![]() 中,
中,![]()
![]() 米,
米,![]() (米),
(米),
即观测点![]() 到灯塔
到灯塔![]() 的距离为
的距离为![]() (米)
(米)
(2)在![]() 中,
中,![]() ,
,
![]() (米),
(米),
在![]() 中,
中,![]() ,
,
![]() (米)
(米)
![]() (米)
(米)
即灯塔![]() ,
,![]() 之间的距离为
之间的距离为![]() (米)
(米)

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目