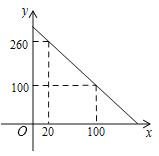
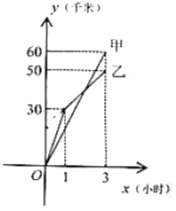
题目内容
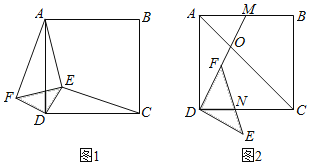
【题目】如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙,无重叠的四边形EFGH,设AB=a,BC=b,若AH=1,则( )
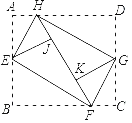
A.a2=4b﹣4B.a2=4b+4C.a=2b﹣1D.a=2b+1
【答案】A
【解析】
利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,根据矩形的性质得到EH=FG,∠A=∠B=∠D=∠C=90°,根据余角的性质得到∠AEH=∠CGF,根据全等三角形的性质得到CF=AH=1,根据相似三角形的性质即可得到结论.
解:∵∠HEJ=∠AEH,∠BEF=∠FEJ,
∴∠HEF=∠HEJ+∠FEJ=![]() ×180°=90°,
×180°=90°,
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形,
∴EH=FG,
∵四边形ABCD是矩形,
∴∠A=∠B=∠D=∠C=90°,
∴∠AEH+∠AHE=∠AHE+∠DHG=∠DHG+∠DGH=∠DGH+∠CGF=90°,
∴∠AEH=∠CGF,
∴△AEH≌△CGF(AAS),
∴CF=AH=1,
∴△AEH∽△BFE,
∴![]() =
=![]() ,
,
由折叠的性质的,AE=EJ=BE=![]() AB=
AB=![]() a,
a,
∴![]() =
=![]() ,
,
∴a2=4b-4,
故选A.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
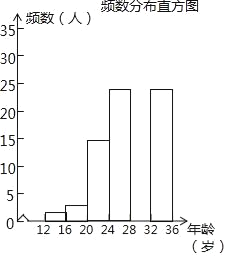
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表
年龄段(岁) | 频数 | 频率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
根据以上信息解答下列问题:
①统计表中的a= ;b= ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?