题目内容
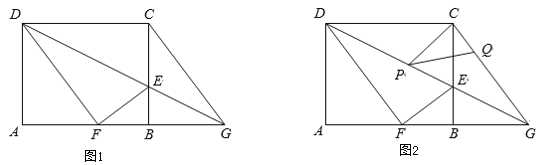
【题目】如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.
(1)求该抛物线的函数解析式.
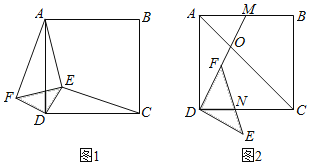
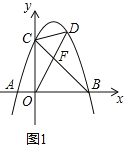
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
(3)如图2,点E的坐标为(0,-2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.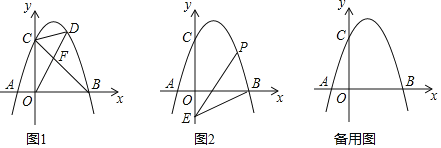
【答案】(1)![]() ;(2)D的坐标为(1,6)或(3,4);(3)(
;(2)D的坐标为(1,6)或(3,4);(3)(![]() )、(
)、(![]() )、(-
)、(-![]() )、(-
)、(-![]() ).
).
【解析】
(1)先根据OB=OC=4.可求得点B、C的坐标,代入y=ax2+3x+c即可求得抛物线解析式;
(2)先运用待定系数法求直线BC解析式,再根据S△COF:S△CDF=4:3,可求得点D、F的横坐标数量关系,根据点F在直线BC上即可表示点F坐标,再运用待定系数法求得直线OF解析式,根据点D在直线OF上即可表示出D的坐标,代入抛物线解析式即可求得点D的坐标;
(3)分四种情况:①当∠PEB=2∠OBE,且点P在x轴上方时,先要构造∠EFO=2∠OBE,可得tan∠OFE=![]() ,再利用解直角三角形知识和解方程组即可求得点P坐标;②当∠PEB=2∠OBE,且点P在x轴下方时,③当∠PBE=2∠OBE,且点P在x轴上方时,④当∠PBE=2∠OBE,且点P在x轴下方时;方法相似.
,再利用解直角三角形知识和解方程组即可求得点P坐标;②当∠PEB=2∠OBE,且点P在x轴下方时,③当∠PBE=2∠OBE,且点P在x轴上方时,④当∠PBE=2∠OBE,且点P在x轴下方时;方法相似.
解:(1)∵OB=OC=4,
∴B(4,0),C(0,4),
把B(4,0),C(0,4)代入y=ax2+3x+c,得![]() ,解得
,解得![]()
∴抛物线的函数解析式为y=-x2+3x+4;
(2)如图1,设直线BC解析式为y=kx+b,则![]() ,解得
,解得![]()
∴直线BC解析式为y=-x+4,
令点D、F的横坐标分别为xD,xF,
∵S△COF:S△CDF=4:3,
∴S△COF=![]() S△COD,即
S△COD,即![]() OCxF=
OCxF=![]() ×
×![]() OCxD,
OCxD,
∴xD=![]() xF,
xF,
设点
∴F(4t,4-4t),
设直线OF解析式为y=k′x,则4-4t=4tk′,
∴k′=![]() ,
,
∴直线OF解析式为y=![]() x,
x,
∵点D在直线OF上,
∴D(7t,7-7t),
将D(7t,7-7t)代入y=-x2+3x+4中,得7-7t=-(7t)2+3×7t+4,解得:t1=![]() ,t2=
,t2=![]() ,
,
∴D的坐标为(1,6)或(3,4);
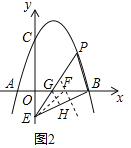
(3)①当∠PEB=2∠OBE,且点P在x轴上方时,如图2,作BE的垂直平分线交OB于F,连接EF,
在∠BEO内部作射线EP交x轴于G,交抛物线于P,使∠PEB=∠EFO,
过点G作GH⊥BE于H,则BF=EF,设BF=EF=m,
∴OF=OB-BF=4-m
在Rt△OEF中,∠EOF=90°,∵OE2+OF2=EF2
∴22+(4-m)2=m2,解得:m=![]() ,
,
∴BF=EF=![]() ,OF=4-
,OF=4-![]() =
=![]() ,
,
∴tan∠OBE=![]() ,tan∠OFE=
,tan∠OFE=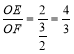 ,
,
∵BF=EF
∴∠BEF=∠OBE
∵∠OFE=∠BEF+∠OBE
∴∠OFE=2∠OBE
∵∠PEB=2∠OBE
∴∠PEB=∠OFE
∴tan∠PEB=![]() ,设GH=4a,则EH=3a,
,设GH=4a,则EH=3a,
∴BE=![]() ,BH=2
,BH=2![]() -3a
-3a
∵![]() =tan∠∠OBE=
=tan∠∠OBE=![]() ,
,
∴![]() ,解得:a=
,解得:a=![]() ,
,
∴GH=![]() ,BH=
,BH=![]()
∴BG=![]()
∴OG=OB-BG=4-![]() =
=![]() ,
,
∴G(![]() ,0),
,0),
设直线EG解析式为y=k″x+b″,则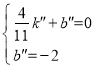 ,解得
,解得 ,
,
∴直线EG解析式为y=![]() x-2,
x-2,
联立方程组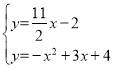 ,解得:
,解得: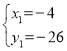 (舍去),
(舍去),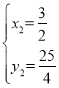 ,
,
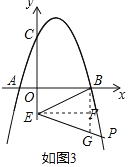
∴P(![]() ),
),
②当∠PEB=2∠OBE,且点P在x轴下方时,如图3,过点E作EF⊥y轴,作点B关于直线EF的对称点G,连接BG交EF于F,
射线EG交抛物线于点P,
∵E(0,-2),
∴直线EF为:y=-2
∵B(4,0),
∴G(4,-4)
∴直线EG解析式为y=-![]() x-2,
x-2,
解方程组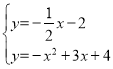 ,得
,得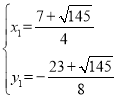 ,
,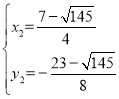 (不符合题意,舍去),
(不符合题意,舍去),
∴P(![]() );
);
③当∠PBE=2∠OBE,且点P在x轴上方时,如图4,
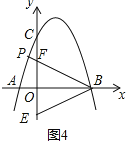
在y轴正半轴上截取OF=OE=2,作射线BF交抛物线于P,
在△BOE和△BOF中,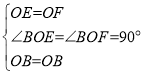
∴△BOE≌△BOF(SAS)
∴∠PBO=∠OBE
∴∠PBE=2∠OBE
易求得直线PF解析式为y=-![]() x+2,
x+2,
联立方程组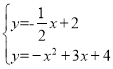 ,解得
,解得![]() (不符合题意,舍去),
(不符合题意,舍去),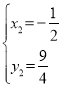 ,
,
∴P(-![]() );
);
④当∠PBE=2∠OBE,且点P在x轴下方时,如图5,
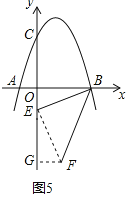
过点E作EF⊥BE交直线BP于F,过F作FG⊥y轴于G,
由①知:tan∠PBE=![]() ,BE=2
,BE=2![]()
∴EF=![]()
∵∠EGF=∠BOE=∠BEF=90°
∴∠BEO+∠FEG=∠BEO+OBE=90°
∴∠FEG=∠OBE
∴△EFG∽△BEO
∴![]() ,即
,即![]()
∴FG=![]() ,EG=
,EG=![]()
∴OG=OE+EG=2+![]() =
=![]()
∴F(![]() ,-
,-![]() )
)
易求得直线BF解析式为y=![]() x-22,
x-22,
联立方程组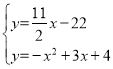 ,解得
,解得![]() (舍去),
(舍去),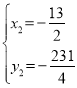 ,
,
∴P(-![]() );
);
综上所述,符合条件的点P的坐标为:(![]() )、(
)、(![]() )、(-
)、(-![]() )、(-
)、(-![]() ).
).