题目内容
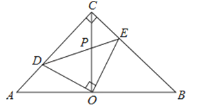
【题目】如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
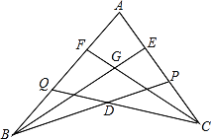
【答案】∠A=80°
【解析】
根据三角形的内角和定理,及角平分线上的性质先计算∠ABC+∠ACB的度数,从而得出∠A的度数.
如图,连接BC.
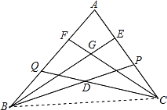
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABE=∠DBE=![]() ∠ABD,∠ACF=∠DCF=
∠ABD,∠ACF=∠DCF=![]() ∠ACD,
∠ACD,
又∠BDC=140°,∠BGC=110°,
∴∠DBC+∠DCB=40°,∠GBC+∠GCB=70°,
∴∠EBD+∠FCD=70°﹣40°=30°,
∴∠ABE+∠ACF=30°,
∴∠ABE+∠ACF+∠GBC+∠GCB=70°+30°=100°,即∠ABC+∠ACB=100°,
∴∠A=80°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目