Question

【题目】如图，点P是正方形ABCD的对角线BD上的一个动点（不与B、D重合），连结AP，过点B作直线AP的垂线，垂足为H，连结DH．若正方形的边长为4，则线段DH长度的最小值是 ．

Answer 1

【答案】2 ﹣2
【解析】解：如图，取AB的中点O，连接OH、OD，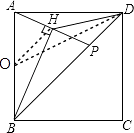
则OH=AO= AB=2，
在Rt△AOD中，OD= = =2 ，
根据三角形的三边关系，OH+DH＞OD，
∴当O、D、H三点共线时，DH的长度最小，
DH的最小值=OD﹣OH=2 ﹣2．
所以答案是：2 ﹣2．
【考点精析】认真审题，首先需要了解正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)，还要掌握点和圆的三种位置关系(圆和点的位置关系：以点P与圆O的为例（设P是一点，则PO是点到圆心的距离），P在⊙O外，PO＞r；P在⊙O上，PO＝r；P在⊙O内，PO＜r)的相关知识才是答题的关键．