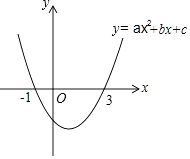题目内容
【题目】如图，抛物线y=x2﹣bx+c过点B（3，0），C（0，﹣3），D为抛物线的顶点．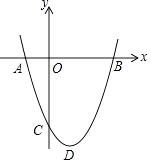
（1）求抛物线的解析式以及顶点坐标；
（2）点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点，连接BC，BE，求∠CBE的正切值；
（3）在（2）的条件下，点M是抛物线对称轴上且在CE上方的一点，是否存在点M使△DMB和△BCE相似？若存在，求点M坐标；若不存在，请说明理由．
【答案】
（1）
解：设抛物线的解析式为y=（x+3）（x+n），将点C的坐标代入得：3n=﹣3，解得n=﹣1．
∴抛物线的解析式为y=（x+3）（x﹣1）即y=x2﹣2x﹣3．
∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴D（1，﹣4）
（2）
解：如图1所示：过点E作ED⊥BC，垂足为D．
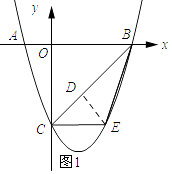
∵B（3，0），C（0，﹣3），
∴OC=OB=3．
∴∠OCB=∠OBC=45°，BC=3 
∵点E与点C关于抛物线的对称轴对称，
∴CE⊥OC，
∴∠DCE=45°．
∵ED⊥CD，
∴△DEB为等腰直角三角形．
∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴抛物线的对称轴为x=1．
∴CE=2．
∴CD=ED= ．
∴BD=BC﹣CD=2 ．
∴tan∠CBE= 
= 
（3）
解：如图2所示：
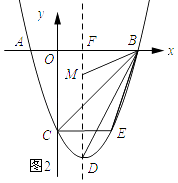
∵B（3，0），D（﹣1，﹣4），
∴A（﹣1，0），F（1，0）．
∴FB=2，DF=4．
∴tan∠FDB= ．
∴tan∠FDB=tan∠CBE．
∴∠FDB=∠CBE．
∴当 
= 
时，△BCE∽△DBM．
∴ 
= 
，解得：MD= 
．
∴点M的纵坐标=﹣4+ =﹣ 
．
∴M（1，﹣ ）．
如图3所示：
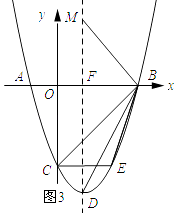
∵∠FDB=∠CBE，
∴当∠BMD=∠BCE=45°时，△DMB∽△BCE．
∴FM=FB=2．
∴M（1，2）．
综上所述，当点M的坐标为（1，﹣ ）或（1，2）时，△DMB和△BCE相似
【解析】（1）设抛物线的解析式为y=（x+3）（x+n），将点C的坐标代入可求得n的值，则可得到抛物线的解析式，然后利用配方法可求得抛物线的顶点坐标；（2）过点E作ED⊥BC，垂足为D．由题意可得到△OBC和△CDE均为等腰直角三角形，然后求得CE、BC、DE的长，最后利用锐角三角函数的定义求解即可；（3）先证明tan∠FDB=tan∠CBE，从而得到∠FDB=∠CBE，当 = 或当∠BMD=∠BCE=45°时，△DMB和△BCE相似．
