题目内容
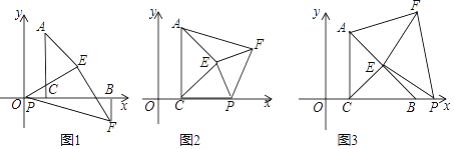
【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF
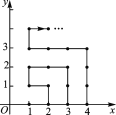
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
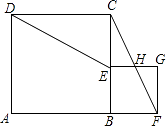
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为________
【答案】(1)①证明见解析②(4,﹣1)(2)证明见解析(3)(4,4)
【解析】
(1)①只要证明∠OEC=∠FEB,OE=EF,EC=EB,即可解决问题.
②由△PCE≌△FBE推出BF=PC=1,只要证明BF⊥PB即可.
(2)如图2中,作PM⊥CE于M,FN⊥EB于N,根据全等三角形的性质可知PM=FN,由S△CPE=![]() CEPM,S△AEF=
CEPM,S△AEF=![]() AEFN,即可证明.
AEFN,即可证明.
(3)由(2)可知△ECP≌△EBF,推出PC=BF,BF⊥CP,由S△CPE=S△AEF,S△AEF=4S△PBE,推出S△CPE=4S△PBE,推出PC=4PB,推出BC=3PB,PB=1,PC=4,推出BF=PC=4,由此即可解决问题.
(1)证明:如图1中,
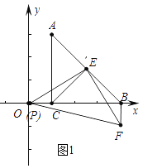
①∵A(1,3),B(4,0),
∴AC=BC=3,△ACB是等腰直角三角形,
∵AE=EB,
∴CE=AE=EB,CE⊥AB,∠ECB=∠EBC=45°,
∴∠CEB=∠OEF=90°,∠ECO=135°,
∴∠OEC=∠FEB,∵OE=EF,EC=EB,
∴△EOC≌△EFB,即△PCE≌△FBE..
②∵△PCE≌△FBE.
∴OC=BF=1,∠EBF=∠OCE=135°,
∴∠OBF=90°,
∴BF⊥OB,
∴F(4,﹣1)
(2)证明:如图2中,作PM⊥CE于M,FN⊥EB于N.
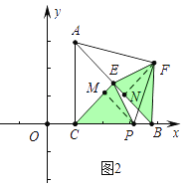
由(1)可知∠OEC=∠FEB,OE=EF,EC=EB,
∴△ECP≌△EBF,
∵PM⊥CE于M,FN⊥EB于N,
∴PM=FN(全等三角形对应边上的高相等),
∵S△CPE=![]() CEPM,S△AEF=
CEPM,S△AEF=![]() AEFN,
AEFN,
∵CE=AE,PM=NF,
∴S△CPE=S△AEF
(3)如图3中,
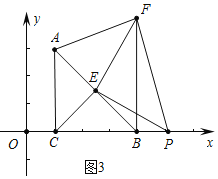
由(2)可知△ECP≌△EBF,推出PC=BF,BF⊥CP,
∵S△CPE=S△AEF,S△AEF=4S△PBE,
∴S△CPE=4S△PBE,
∴PC=4PB,
∴BC=3PB,PB=1,PC=4,
∴BF=PC=4,
∴点F坐标为(4,4).
故答案为(4,4).