题目内容
【题目】如图,![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() ,
,![]()

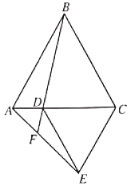

图1 图2 图3
(1)如图一,证明:![]()
(2)如图二,如果![]() 在
在![]() 边上,
边上,![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.
(3)如图三,在(2)的条件下,过![]() 作
作![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)10
;(3)10
【解析】
(1)先根据等边三角形的性质得出![]() ,再根据角的和差得出
,再根据角的和差得出![]() ,然后根据三角形全等的判定定理与性质即可得证;
,然后根据三角形全等的判定定理与性质即可得证;
(2)先根据三角形全等的判定定理与性质得出![]() ,再根据对顶角相等、三角形的外角性质即可得;
,再根据对顶角相等、三角形的外角性质即可得;
(3)如图(见解析),连接![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() ,先根据等边三角形的判定与性质得出
,先根据等边三角形的判定与性质得出![]() ,再根据角的和差求出
,再根据角的和差求出![]() ,然后根据三角形全等的判定定理与性质得出
,然后根据三角形全等的判定定理与性质得出![]() ,最后根据线段的和差、直角三角形的性质求出
,最后根据线段的和差、直角三角形的性质求出![]() 的长,由此即可得出答案.
的长,由此即可得出答案.
(1)![]() 和
和![]() 均为等边三角形
均为等边三角形
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,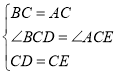
![]()
![]() ;
;
(2)![]() 和
和![]() 均为等边三角形
均为等边三角形
![]()
在![]() 和
和![]() 中,
中,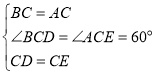
![]()
![]()
![]()
![]()
![]()
故![]() 的度数为
的度数为![]() ;
;
(3)如图,连接![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]()
由(2)可知:![]()
![]() 是等边三角形
是等边三角形
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,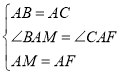
![]()
![]()
![]()
![]()
由(2)可知:![]()
![]()
![]()
![]()
又![]()
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
即![]() 的长为10.
的长为10.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
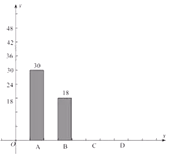
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共________人, ![]() ________,
________, ![]() ________;
________;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有________人.