Question

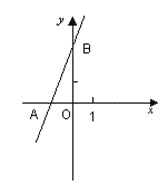
【题目】如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.

（1）求A，B两点的坐标；

（2）过B点作直线BP与x轴相交于P，且使OP=2OA， 求ΔABP的面积.

Answer 1

【答案】（1）A（，0），B(0，3)；（2）或

【解析】

(1) 根据坐标轴上点的坐标特征求A点和B点坐标；

(2) 有两种情况，若BP与x轴正方向相交于P点，则AP=3OA；若BP与x轴负方向相交于P点，则AP=OA，由此求得△ABP的面积．

解(1)令y=0，得x=∴A点坐标为(，0).令x=0，得y=3

∴B点坐标为(0，3).

(2)设P点坐标为(x，0)，依题意，得x=±3.

∴P点坐标为P1(3，0)或P2(－3，0).∴S△ABP1==

S△ABP2==. ∴△ABP的面积为或.