题目内容
如图，在四边形ABCD中，AB＝BC，对角线BD平分ÐABC，P是BD上一点，过点P作PM^AD，PN^CD，垂足分别为M、N.
（1）求证：ÐADB＝ÐCDB；
（2）若ÐADC＝90°，求证：四边形MPND是正方形.
（1）求证：ÐADB＝ÐCDB；
（2）若ÐADC＝90°，求证：四边形MPND是正方形.
（1）证明见解析；（2）证明见解析.
试题分析：（1）根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD，由全等三角形的性质即可得到：∠ADB=∠CDB；（2）若∠ADC=90°，由（1）中的条件可得四边形MPND是矩形，再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
试题解析：（1）∵BD平分ÐABC，∴ÐABD=ÐCBD.
又∵BA=BC，BD=BD，∴△ABD ≌△CBD（SAS）.∴ÐADB=ÐCDB.
（2）∵PM^AD，PN^CD，∴ÐPMD=ÐPND=90°.
又∵ÐADC=90°，∴四边形MPND是矩形.
∵ÐADB=ÐCDB，PM^AD，PN^CD，∴PM="PN." ∴四边形MPND是正方形.
练习册系列答案
相关题目
．根据这个结论，解决下面问题：在梯形ABCD中，∠B=45°，AD//BC，AB=5，AD=4，BC=
，P是线段BC上一动点，点P从点B出发，以每秒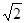
个单位的速度向C点运动．
