Question

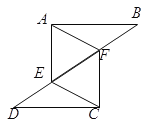
【题目】如图，A，B，C三点在⊙O上，直径BD平分∠ABC，过点D作DE∥AB交弦BC于点E，在BC的延长线上取一点F，使得EFDE．

（1）求证：DF是⊙O的切线；

（2）连接AF交DE于点M，若 AD4，DE5，求DM的长．

Answer 1

【答案】（1）证明见解析；（2）1

【解析】试题分析：

（1）由BD平分∠ABC，AB∥DE可证得∠DBE=∠BDE，由DE=EF，可得∠EDF=∠EFD，由此可得∠BDE+∠EDF=90°，即可得到BD⊥DF，从而可得DF是⊙O的切线；

（2）如图，连接DC，由已知易证△ABD≌△CBD，从而可得 CD=AD=4，AB=BC；在Rt△DCE中由勾股定理可求得EC=3；由（1）可得BE=DE=EF=5，从而可得BC=AB=8；由AB∥DE可得△ABF∽△MEF，由此即可求得ME的长，最后由MD=DE-ME即可求得所求答案.

试题解析：

（1）∵ BD平分∠ABC，

∴ ∠ABD=∠CBD.

∵ DE∥AB，

∴ ∠ABD=∠BDE.

∴ ∠CBD=∠BDE.

∵ ED=EF，

∴ ∠EDF=∠EFD.

∵∠EDF+∠EFD+∠EDB+∠EBD=180°，

∴ ∠BDF=∠BDE+∠EDF=90°.

∴ OD⊥DF.

∵OD是半径，

∴ DF是⊙O的切线.

（2）连接DC，

∵ BD是⊙O的直径，

∴ ∠BAD=∠BCD=90°.

∵ ∠ABD=∠CBD，BD=BD，

∴ △ABD≌△CBD.

∴ CD=AD=4，AB=BC.

∵ DE=5，

∴，EF=DE=5.

∵ ∠CBD=∠BDE，

∴ BE=DE=5.

∴， .

∴ AB=8.

∵ DE∥AB，

∴ △ABF∽△MEF.

∴.

∴ ME=4.

∴.