题目内容
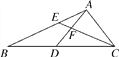
【题目】如图,在△ABC中,点D,E分别在边BC,AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF·EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF·AD=AB·EF.
【答案】详见解析.
【解析】试题分析:(1)、根据已知条件的线段比值以及∠AEF=∠CEA得出△EAF和△ECA相似,从而得出∠EAF=∠ECA,根据AD=AC得出∠ADC=∠ACD,从而得出角度之间的关系;(2)、根据第一题中的相似得出∠EFA=∠CAB,根据BD=AD得出∠B=∠EAF,从而得出△FAE和△ABC相似,即![]() ,根据AC=AD得出结论.
,根据AC=AD得出结论.
试题解析:(1)∵AE2=EF·EC, ∴![]() =
=![]() , 又∵∠AEF=∠CEA, ∴△EAF∽△ECA,
, 又∵∠AEF=∠CEA, ∴△EAF∽△ECA,
∴∠EAF=∠ECA. ∵AD=AC, ∴∠ADC=∠ACD.
∵∠ACD=∠DCE+∠ECA=∠DCE+∠EAF, ∴∠ADC=∠DCE+∠EAF;
(2)由(1)可知△EAF∽△ECA, ∴∠EFA=∠EAC, 即∠EFA=∠CAB.
∵BD=AD, ∴∠B=∠BAD,即∠B=∠EAF, ∴△FAE∽△ABC,
∴![]() =
=![]() , ∴FA·AC=AB·FE, ∵AC=AD, ∴AF·AD=AB·EF.
, ∴FA·AC=AB·FE, ∵AC=AD, ∴AF·AD=AB·EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




