��Ŀ����
����Ŀ����ͼ1��ʾ����һ��������ֽƬABC����֪��ACB=90��,AC=24,BC=10,AB=26,��DΪAB����һ�㣬����CD��AD=CD=DB����CD������ֽƬ������![]() ����
����![]() ������������ͼ2��ʾ����ֽƬ��
������������ͼ2��ʾ����ֽƬ��![]() ��ֱ��
��ֱ��![]() ����ƽ�ƣ���A��
����ƽ�ƣ���A��![]() ʼ�ն���ͬһֱ���ϣ���
ʼ�ն���ͬһֱ���ϣ���![]() ��
��![]() ���ڵ�E��
���ڵ�E��![]() ��
��![]() ��
��![]() �ֱ��ڵ�E��F��
�ֱ��ڵ�E��F��
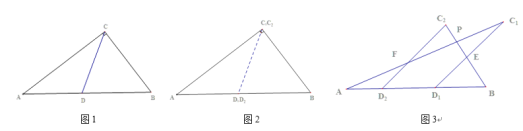
��1������A![]() ƽ�ƹ����У���֤��
ƽ�ƹ����У���֤��![]()
��2������A![]() ƽ�Ƶ���ͼ3��ʾ��λ��ʱ������ͼ�е�
ƽ�Ƶ���ͼ3��ʾ��λ��ʱ������ͼ�е�![]() ������ϵ��������֤����
������ϵ��������֤����
��3����ƽ�ƾ���![]() Ϊx����ƽ�ƹ����У�AP=
Ϊx����ƽ�ƹ����У�AP=![]() AB��PB=
AB��PB=![]() AB���������APB���������ԭ��ABC���һ��ʱ��xֵ��
AB���������APB���������ԭ��ABC���һ��ʱ��xֵ��
���𰸡���1������������2��D1E��D2F��֤������������3��![]() .
.
��������
��1������ƽ�Ƶ����ʿɵ�AC��AC1��Ȼ���ϡ�ACB=90����֤�ý��ۣ�
��2������ƽ���ߵ����ʺ͵ȱ߶ԵȽǿɵá�AFD2����A��Ȼ��ɵ�AD2��D2F��ͬ�����BD1��D1E��Ȼ�������߶κͲ�֤��AD2��BD1���ɵõ�D1E��D2F��
��3������ƽ�ƾ���Ϊx�ɵ�AB��26-x��Ȼ���ʾ��AP��PB��������APB���������ԭ��ABC���һ���г����̲���⣬��ȥ���������ֵ���ɵó����.
�⣺��1������ƽ�Ƶ����ʿɵ�AC��AC1��
�ߡ�ACB=90������AC��BC��
��AC1��BC����![]() ��
��
��2��D1E��D2F��
֤������C1D1��C2D2��
���C1����AFD2��
�֡�AD=CD=DB����C1D1��C2D2��BD2��AD1��
���C1����A��
���AFD2����A��
��AD2��D2F��
ͬ����BD1��D1E��
�֡�AD1��BD2��
��AD2��BD1��
��D1E��D2F��
��3����ƽ�ƾ���![]() Ϊx��
Ϊx��
��AB��26-x��
��AP=![]() AB=
AB=![]() ��PB=
��PB=![]() AB=
AB=![]() ��
��
������ã�![]() ��
��
�����ã�![]() ��
��
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
����APB���������ԭ��ABC���һ��ʱ��xֵΪ![]() .
.

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�����Ŀ�����죬С�����Լ��Ҹո�װ��ˮ����ʾ�¶�Ϊ![]() ��̫������ˮ�����ˮ����.��ÿ��һ��ʱ��ȥ�۲�һ����ʾ�¶ȣ�����¼���£�
��̫������ˮ�����ˮ����.��ÿ��һ��ʱ��ȥ�۲�һ����ʾ�¶ȣ�����¼���£�
ʱ�䣨���ӣ� | 0 | 5 | 10 | 15 | 20 | ���� |
��ʾ�¶ȣ� | 16 | 17 | 18 | 19 | 20 | ���� |
��1����ֱ��д����ʾ�¶ȣ�![]() �������ʱ�䣨
�������ʱ�䣨![]() ��֮��ĺ�����ϵʽ��
��֮��ĺ�����ϵʽ��
��2�����������ˮ���趨������¶�Ϊ![]() ���ʣ�Ҫ���ȶʱ����ܴﵽ�趨������¶ȣ�
���ʣ�Ҫ���ȶʱ����ܴﵽ�趨������¶ȣ�