Question

【题目】如图，在等腰直角△ABC中，∠C=90°，点O是AB的中点，且AB=，将一块直角三角板的直角顶点放在点O处，始终保持该三角板的两直角边分别与AB、BC相交，交点分别为D、E，则CD+CE=（ ）

A.B.C.2D.

Answer 1

【答案】A

【解析】

连接OC构建全等三角形，证明△ODC≌△OEB，得DC=BE；把CD+CE转化到同一条线段上，即求BC的长；通过等腰直角△ABC中斜边AB的长就可以求出BC=，则CD+CE=BC=．

连接OC，

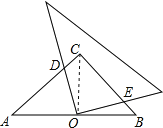
∵等腰直角△ABC中，AB=，
∴∠B=45°，
∴cos∠B=，
∴BC=×cos45°= ，
∵点O是AB的中点，
∴OC=AB=OB，OC⊥AB，
∴∠COB=90°，
∵∠DOC+∠COE=90°，∠COE+∠EOB=90°，
∴∠DOC=∠EOB，
同理得∠ACO=∠B，
∴△ODC≌△OEB，
∴DC=BE，
∴CD+CE=BE+CE=BC=，
故选：A．