题目内容
【题目】如图，已知二次函数
的图象过点
和点
，对称轴为直线
．
求该二次函数的关系式和顶点坐标；
结合图象，解答下列问题：
①当
时，求函数
的取值范围．
②当
时，求
的取值范围．
【答案】(1)
抛物线的顶点坐标为
；(2)①当
时，
；②当
时，
或
．
【解析】
（1）把A点和C点坐标代入y=ax2+bx+c得到两个方程，再加上对称轴方程即可得到三元方程组，然后解方程组求出a、b、c即可得到抛物线解析式，再把解析式配成顶点式即可得到顶点坐标；
（2）①先分别计算出x为-1和2时的函数值，然后根据二次函数的性质写出对应的函数值的范围；
②先计算出函数值为3所对应的自变量的值，然后根据二次函数的性质写出y＜3时，x的取值范围．
解：
根据题意得
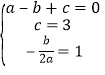，解得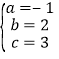
，
所以二次函数关系式为
，
因为
，
所以抛物线的顶点坐标为；
①当
时，
；
时，
；
而抛物线的顶点坐标为，且开口向下，
所以当时，；
②当时，
，解得
或
，
所以当时，或．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
