题目内容
【题目】在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化．如图，四边形的顶点在矩形的边上，且AN=AM=CP=CQ=xcm，已知矩形的边BC=200m，边AB=am，a为大于200的常数，设四边形MNPQ的面积为sm2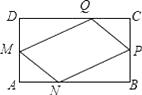
（1）求S关于x的函数关系式，并直接写出自变量x的取值范围．
（2）若a=400，求S的最大值，并求出此时x的值．
【答案】
（1）解：由题意S=200a﹣2× 
x2﹣2× （200﹣a）（a﹣x）=﹣2x2+（200+a）x（0＜x＜a）
（2）解：∵a=400，
∴S=﹣2x2+600x=﹣2（x﹣150）2+45000．
∴x=150时，S最大值=45000，
∴S最大值为45000cm2 ， 此时x=150cm
【解析】考查二次函数的应用.小题1 根据四边形MNPQ的面积=矩形ABCD的面积-4个三角形面积计算即可． 小题2 利用配方法求出二次函数的最值．
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
【题目】某服装店用6000元购进A，B两种新式服装，按标价售出后可获得毛利润3800元（毛利润＝售价﹣进价），这两种服装的进价、标价如下表所示：
类型 价格 | A型 | B型 |
进价（元/件） | 60 | 100 |
标价（元/件） | 100 | 160 |
（1）求这两种服装各购进的件数；
（2）如果A中服装按标价的8折出售，B中服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价售出少收入多少元？
【题目】某公司有A、B两种型号的客车共11辆，它们的载客量（不含司机）、日租金、车辆数如下表所示，已知这11辆客车满载时可搭载乘客350人．
A型客车 | B型客车 | |
载客量（人/辆） | 40 | 25 |
日租金（元/辆） | 320 | 200 |
车辆数（辆） | a | b |
（1）求a、b的值；
（2）某校七年级师生周日集体参加社会实践，计划租用A、B两种型号的客车共6辆，且租车总费用不超过1700元．
①最多能租用A型客车多少辆？
②若七年级师生共195人，写出所有的租车方案，并确定最省钱的租车方案．
