Question

【题目】如图，已知AB∥ED，设∠A＋∠E＝α，∠B＋∠C＋∠D＝β，则( )

A. α－β＝0B. 2α－β＝0C. α－2β＝0D. 3α－2β＝0

Answer 1

【答案】B

【解析】

过点C作CF∥AB，根据平行的传递性可得CF∥ED，由平行线的性质：两直线平行，同旁内角互补，得∠D+∠ DCF=180°，∠B+∠ BCF=180°，∠A+∠ E=180°，从而可得2α-β=0.

过点C作CF∥AB，如图，

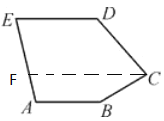
∵AB∥ ED，CF∥ AB，

∴CF∥ED，

∴∠ D+∠ DCF=180°，

∵CF∥AB，

∴∠ B+∠ BCF=180°，

∴∠ β=∠ B+∠ BCD+∠ D=∠ B+∠ B CF+∠ DCF+∠ D=360°，

∵AB∥ED，

∴∠A+∠ E=180°，

∴2α-β=0.

故答案为：B.