题目内容
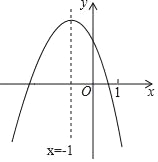
【题目】在平面直角坐标系中，二次函数y=ax2+bx+c的图象开口向上，且经过点A（0，
）．
（1）若此函数的图象经过点（1，0）、（3，0），求此函数的表达式；
（2）若此函数的图象经过点B（2，﹣
），且与x轴交于点C、D．
①填空：b=_____（用含α的代数式表示）；
②当CD2的值最小时，求此函数的表达式．
【答案】﹣2a-1；
【解析】分析：
用待定系数法即可求出函数的表达式.
①把A点坐标代入二次函数解析式可求得
把B点坐标代入可得
整理即可得到
②设
由根与系数的关系得到
根据二次函数的性质，即可求出
的值，进而求得此时的函数表达式.
详解：（1）由题意可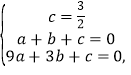得
，解得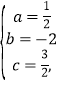
，
∴函数表达式为
（2）①把A点坐标代入二次函数解析式可求得
把B点坐标代入可得
∴
故答案为：
②设
由①可得二次函数表达式为
令
可得
∴
令
由抛物线开口向上可知
，则
∴
∴当
时，
有最小值，此时
∴当有最小值时，二次函数表达式为
练习册系列答案
优学名师名题系列答案
相关题目
