题目内容
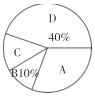
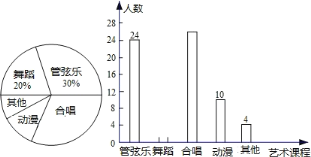
【题目】某中学七年级开设了艺术课程,每名学生从合唱、管弦乐、舞蹈、动漫、吉他这五门课程中选择一门进行学习.为了解学生的选择意向,从七年级随机抽取了若干名同学进行了调查,将调查得到的结果绘制成如图所示的两幅统计图(均不完整).
根据题中信息,回答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)若该校七年级一共有 240 名学生,请估计其中有多少人会选择合唱课程.
【答案】(1)在这次调查中,一共抽取了80名学生;(2)补图见解析;(3)估计其中有78人会选择合唱课程.
【解析】
(1)根据选择管弦乐的有24人,所占的百分比是30%,据此即可求得抽取的总人数;
(2)利用百分比的意义求得选择舞蹈的人数,即可补全条形统计图;
(3)利用七年级学生总数乘以选择合唱课程的比例即可.
(1)抽取的总人数是:24÷30%=80(人);
(2)选择舞蹈的人数是:80×20%=16(人),选择合唱的人数是80-24-16-10-4=26(人),
条形统计图如下: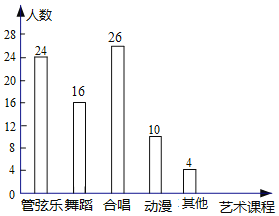
(3)240×![]() =78(人).
=78(人).
答:估计该校七年级学生选择合唱课程的人数是 78 人.

 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
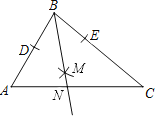
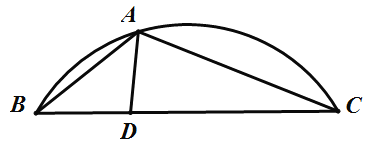
学而优暑期衔接南京大学出版社系列答案【题目】如图,A是![]() 上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是
上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是![]() cm,线段AD的长是
cm,线段AD的长是![]() cm.
cm.
小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:
随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点A在![]() 上的不同位置,画图、测量,得到了
上的不同位置,画图、测量,得到了![]() ,
,![]() 的长度与x的几组值:
的长度与x的几组值:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
x/cm | 0.00 | 0.99 | 2.01 | 3.46 | 4.98 | 5.84 | 7.07 | 8.00 |
| 8.00 | 7.46 | 6.81 | 5.69 | 4.26 | 3.29 | 1.62 | 0.00 |
| 2.50 | 2.08 | 1.88 | 2.15 | 2.99 | 3.61 | 4.62 | m |
请直接写出上表中的m值是 ;
(2)在同一平面直角坐标系![]() 中,描出补全后表中各组数据所对应的点(x,
中,描出补全后表中各组数据所对应的点(x,![]() ),(x,
),(x,![]() ),并画出函数
),并画出函数![]() ,
,![]() 的图象;
的图象;
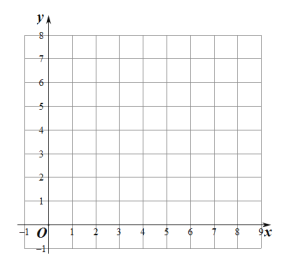
(3)结合函数图象,解决问题:当AC=AD时,AB的长度约为 cm;当AC=2AD时,AB的长度约为 cm.