题目内容
【题目】已知函数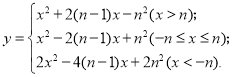 其中
其中![]() 是常数,且
是常数,且![]() >0.
>0.
(1)若点(![]() ,2)在函数的图象上,求
,2)在函数的图象上,求![]() 的值.
的值.
(2)当![]() =1时,①当
=1时,①当![]() ≤
≤![]() ≤2时,求函数值
≤2时,求函数值![]() 的取值范围.
的取值范围.
②当![]() ≤
≤![]() ≤
≤![]() 时,函数图象上的点到
时,函数图象上的点到![]() 轴的距离恒(永远)小于6,求
轴的距离恒(永远)小于6,求![]() 的取值范围.
的取值范围.
(3)直接写出函数图象与![]() 有两个交点时的
有两个交点时的![]() 取值范围.
取值范围.
【答案】(1)![]() 或
或![]() ;(2)①0<
;(2)①0<![]() ≤3,4<
≤3,4<![]() ≤10; ②
≤10; ② ![]() ≤
≤![]() ≤
≤![]() ;(3)
;(3)![]() ,
,![]() ≤
≤![]() <
<![]() ,
,![]() <
<![]() <
<![]()
【解析】
(1)根据题意,把点(![]() ,2)分别代入解析式,求出n的值,然后结合n的取值范围,即可得到答案.
,2)分别代入解析式,求出n的值,然后结合n的取值范围,即可得到答案.
(2)①当n=1时,求出代数式,然后根据x的取值范围,分别求出y的取值范围,即可得到答案;
②结合图像y=6与函数图像的交点,找出临界点,然后根据函数图象上的点到![]() 轴的距离恒(永远)小于6,即可求出t的取值范围;
轴的距离恒(永远)小于6,即可求出t的取值范围;
(3)根据题意,可分为两种情况:当![]() 时,先计算函数的顶点坐标,纵坐标相等,然后求出n的值;当
时,先计算函数的顶点坐标,纵坐标相等,然后求出n的值;当![]() 时,找出有两个交点时的临界点,然后通过计算,求出n的取值范围,即可得到答案.
时,找出有两个交点时的临界点,然后通过计算,求出n的取值范围,即可得到答案.
解:(1)当点(![]() ,2)在函数
,2)在函数![]() 时,
时,
有![]() ,
,
解得:![]() (不符合题意,舍去);
(不符合题意,舍去);
当点(![]() ,2)在函数
,2)在函数![]() 的图象上时,
的图象上时,
有![]() ,
,
解得:![]() (负值舍去),
(负值舍去),
∴![]() ;
;
当点(![]() ,2)在函数
,2)在函数![]() 的图象上时,
的图象上时,
有![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
综上所述,![]() 或
或![]() .
.
(2)当![]() 时,
时,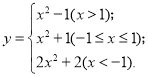
①当![]() ≤
≤![]() ≤2时,有
≤2时,有![]() ≤
≤![]() <
<![]() ,
,![]() ≤
≤![]() ≤1,1<
≤1,1<![]() ≤2三段.
≤2三段.
取![]() ≤
≤![]() <
<![]() 时,有
时,有![]() ,
,
∴4<![]() ≤10;
≤10;
取![]() ≤
≤![]() ≤1,有
≤1,有![]() ,
,
∴1≤![]() ≤2;
≤2;
取1<![]() ≤2,有
≤2,有![]() ,
,
∴0<![]() ≤3.
≤3.
∴ 综上所述,0<![]() ≤3,4<
≤3,4<![]() ≤10.
≤10.
②当![]() =1时,函数图象如图所示.
=1时,函数图象如图所示.
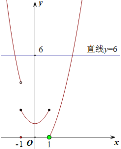
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,![]() (舍去);
(舍去);
当![]() ,
,
解得:![]() (舍去),
(舍去),![]() ;
;
∴![]() ≤
≤![]() ≤
≤![]() 时,
时,![]() ≤6.
≤6.
∴ 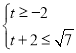 ,
,
∴ ![]() ≤
≤![]() ≤
≤![]() .
.
(3)∵![]() ,
,
∴ 顶点坐标是(![]() ,
,![]() );
);
∵![]() ,
,
∴顶点坐标是(![]() ,
,![]() );
);
∴![]() =
=![]() ,
,
解得:![]() (负值舍去),
(负值舍去),
∴![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() =
=![]() ,
,
解得:![]() ,.
,.
∵![]() ,解得:
,解得:![]() ,
,
结合![]() ,
,![]() .
.
∴函数图象与![]() 有两个交点时,
有两个交点时,![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ≤
≤![]() <
<![]() 或
或![]() <
<![]() <
<![]() .
.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查过程如下,请补充完整,
收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65
乙班:90,55,80,70,55,70,95,80,65,70
(1)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x人数班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=________;n=________.
(2)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 75 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=________,y=________.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀请估计乙班50名学生中身体素质为优秀的学生有________人.
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从有400人的某小区抽取40名人员的答卷成绩,并对他们的成绩(单位:分)统计如下:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
80 | 60 | 80 | 95 | 85 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
根据数据绘制了如下的表格和统计图:
等级 | 成绩( | 频率 | 频率 |
|
| 10 | 0.25 |
|
|
| |
|
| 12 | 0.3 |
|
|
| |
合计 | 40 | 1 | |
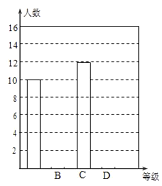
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
(4)该社区有2名男管理员和2名女管理员,现从中随机挑选2名管理员参加“社区防控”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.