Question

【题目】（1）问题发现

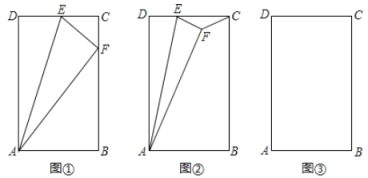
如图1，是等边三角形，点，分别在边，上．若，则，，，之间的数量关系是 ；

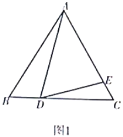
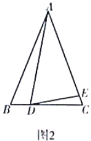
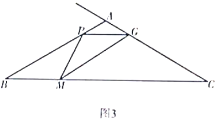
（2）拓展探究

如图2，是等腰三角形，，，点，分别在边，上．若，则（1）中的结论是否仍然成立？请说明理由．

（3）解决问题

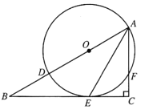
如图3，在中，，，点从点出发，以img src="https://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿方向匀速运动，同时点从点出发，以的速度沿方向匀速运动，当其中一个点运动至终点时，另一个点随之停止运动．连接，在右侧作，该角的另一边交射线于点，连接．设运动时间为，当为等腰三角形时，直接写出的值．

Answer 1

【答案】（1）；（2）成立，见详解；（3）1或2．

【解析】

（1）通过角的关系可证△ABD∽△DCE，根据相似三角形对应边成比例可得到线段的关系；

（2）同（1）中的思路相同，通过角的关系可证△ABD∽△DCE，即可得到结论；

（3）可证△PBM∽△MCG，然后得到,用来表示线段的长，当G点在线段AC上时，若为等腰三角形时，则AP=AG，代入计算即可；当G点在CA延长线上时，若为等腰三角形时，则为等边三角形，代入计算得到．

（1），

∵是等边三角形，

∴∠B=∠C=60°，

∴∠BAD+∠ADB=180°-60°=120°，

，

∴∠CDE+∠ADB=180°-60°=120°，

∴∠BAD=∠CDE，

∴△ABD∽△DCE，

∴；

（2）成立，

∵，，

∴，

∴∠BAD+∠ADB=，

∵，

∴∠CDE+∠ADB=，

∴∠BAD=∠CDE，

∴△ABD∽△DCE，

∴；

（3）∵，，

∴∠B=∠C=30°，

∴∠BPM+∠PMB=180°-30°=150°，

∵，

∴∠CMG+∠PMB=180°-30°=150°，

∴∠BPM=∠CMG，

又∠B=∠C=30°，

∴△PBM∽△MCG，

∴，

由题意可知， ，即，

如图，过点A作AH⊥BC于H，

∵，，

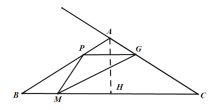
∴AH=2，，

∵，AH⊥BC，

∴，

∴，

∴，即，

当G点在线段AC上时，若为等腰三角形时，则AP=AG，如图3，

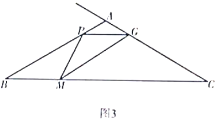
此时AG=AC-CG=，

∴，解得，

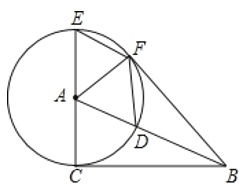
当G点在CA延长线上时，若为等腰三角形时，如下图，

此时∠PAG=180°-120°=60°，则为等边三角形，AP=AG，

此时AG=CG-AC=，

∴，解得，

∴当为等腰三角形时，的值为1或2．