题目内容
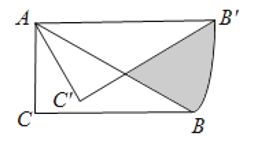
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的点,连接
上的点,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折得
翻折得![]() .
.
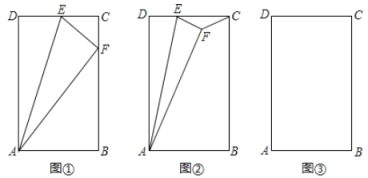
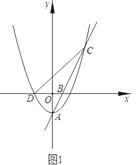
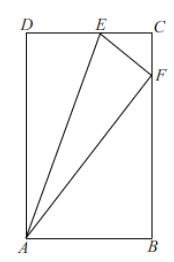
(1)如图①,点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() ∽
∽![]() ;
;
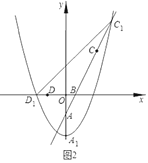
(2)如图②,点![]() 在矩形
在矩形![]() 内,连接
内,连接![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)若以点![]() 、
、![]() 、
、![]() 为顶点的三角形是直角三角形,则
为顶点的三角形是直角三角形,则![]() 的长为 .
的长为 .
【答案】(1)见解析;(2)![]() 的面积为
的面积为![]() ;(3)
;(3)![]() 、5、15、
、5、15、![]()
【解析】
(1)先说明∠CEF=∠AFB和![]() ,即可证明
,即可证明![]() ∽
∽![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 与点
与点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ;再结合矩形的性质,证得△FGE∽△AHF,得到AH=5GF;然后运用勾股定理求得GF的长,最后运用三角形的面积公式解答即可;
;再结合矩形的性质,证得△FGE∽△AHF,得到AH=5GF;然后运用勾股定理求得GF的长,最后运用三角形的面积公式解答即可;
(3)分点E在线段CD上和DC的延长线上两种情况,然后分别再利用勾股定进行解答即可.
(1)解:∵矩形![]() 中,
中,
∴![]()
由折叠可得![]()
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]() ,
,![]()
∴![]() ∽
∽![]()
(2)解:过点![]() 作
作![]() 交
交![]() 与点
与点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]()
∵矩形![]() 中,
中,
∴![]()
由折叠可得:![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
∴![]()
在![]() 中,
中,![]()
∵![]()
∴![]()
∴![]()
∴![]() 的面积为
的面积为![]()
(3)设DE=x,以点E、F、C为顶点的三角形是直角三角形,则:
①当点E在线段CD上时,∠DAE<45°,
∴∠AED>45°,由折叠性质得:∠AEF=∠AED>45°,
∴∠DEF=∠AED+∠AEF>90°,
∴∠CEF<90°,
∴只有∠EFC=90°或∠ECF=90°,
a,当∠EFC=90°时,如图所示:

由折叠性质可知,∠AFE=∠D=90°,
∴∠AFE+∠EFC=90°,
∴点A,F,C在同一条线上,即:点F在矩形的对角线AC上,
在Rt△ACD中,AD=5,CD=AB=3,根据勾股定理得,AC=![]() ,
,
由折叠可知知,EF=DE=x,AF=AD=5,
∴CF=AC-AF=![]() -5,
-5,
在Rt△ECF中,EF2+CF2=CE2,
∴x2+(![]() -5)2=(3-x)2,解得x=
-5)2=(3-x)2,解得x=![]() 即:DE=
即:DE=![]()
b,当∠ECF=90°时,如图所示: 点F在BC上,由折叠知,EF=DE=x,AF=AD=5,
在Rt△ABF中,根据勾股定理得,BF=![]() =4,
=4,
∴CF=BC-BF=1,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
(3-x)2+12=x2,解得x=![]() ,即:DE=
,即:DE=![]() ;
;
②当点E在DC延长线上时,CF在∠AFE内部,而∠AFE=90°,
∴∠CFE<90°,
∴只有∠CEF=90°或∠ECF=90°,
a、当∠CEF=90°时,如图所示

由折叠知,AD=AF=5,∠AFE=90°=∠D=∠CEF,
∴四边形AFED是正方形,
∴DE=AF=5;
b、当∠ECF=90°时,如图所示:
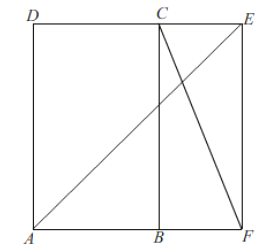
∵∠ABC=∠BCD=90°,
∴点F在CB的延长线上,
∴∠ABF=90°,由折叠知,EF=DE=x,AF=AD=5,
在Rt△ABF中,根据勾股定理得,BF=![]() =4,
=4,
∴CF=BC+BF=9,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
∴(x-3)2+92=x2,解得x=15,即DE=15,
故答案为![]() 、
、![]() 、5、15.
、5、15.

【题目】为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:7,8,7,8,9,9; 小亮:5,8,7,8,10,10.
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
小华 | 8 | ||
小亮 | 8 | 3 |
(2)根据以上信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,分别命中7环和9环,则小亮这8次射击成绩的方差 .(填“变大”、“变小”、“不变”)
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有400名学生进入综合素质展示环节.为了了解两所学校这些学生的整体情况,从两校进人综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
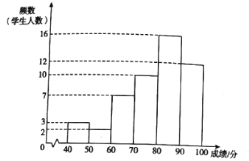
b.甲学校学生成绩在![]() 这一组的是:
这一组的是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生A,乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是______(填“A”或“B”);
(2)根据上述信息,推断_____学校综合素质展示的水平更高,理由为_____(至少从两个不同的角度说明推断的合理性);
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到____分的学生才可以入选.