题目内容
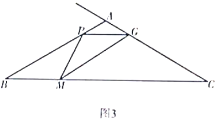
【题目】如图,△ABC内接于⊙O,AB=AC,BD为⊙O的直径,过点A作AE⊥BD于点E,延长BD交AC延长线于点F.
(1)若AE=4,AB=5,求⊙O的半径;
(2)若BD=2DF,求sin∠ACB的值.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)连接OA,在Rt△ABE中,利用勾股定理求得BE的长,设半径为![]() , 在Rt△OAE中,利用勾股定理构建方程即可求解;
, 在Rt△OAE中,利用勾股定理构建方程即可求解;
(2)连接CD,设OA交BC于点H,先证得OA⊥BC,推出OH//CD,设OH=![]() ,推出CD=
,推出CD=![]() ,OA=
,OA=![]() ,AH=
,AH=![]() ,利用勾股定理求得
,利用勾股定理求得![]() ,
,![]() ,即可求解.
,即可求解.
(1)连接OA,
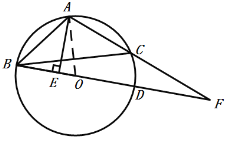
∵AE=4,AB=5,AE⊥BD,
∴![]() ,即
,即![]() ,
,
∴BE=3,
设⊙O半径为![]() ,
,
在Rt△OAE中,OA=OB=![]() ,OE=
,OE=![]() ,AE=4,
,AE=4,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴⊙O半径为![]() ;
;
(2)连接CD、OA,设OA交BC于点H,
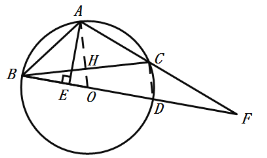
∵AB=AC,
∴![]() =
=![]() ,即点A为
,即点A为![]() 的中点,
的中点,
∴OA垂直平分BC,
∴OA⊥BC,
∵BD为直径,
∴∠BCD=90![]() ,
,
∵∠BHO=∠BCD=90![]() ,BO=OD,
,BO=OD,
∴OH//CD,CD =2OH,
设OH=![]() ,则CD=
,则CD=![]() ,
,
∵BD=2DF,
∴OD=DF,
∴CD =![]() OA,
OA,
∴OA=![]() ,
,
则AH=![]() ,
,
在Rt△BOH中,OB=OA=![]() ,OH=
,OH=![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在Rt△BAH中,![]() ,
,
∴![]() ,
,
∵AB=AC,
∴sin∠ACB= ![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目