题目内容
(7分)
关于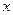 的方程为
的方程为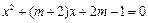 .
.
(1)证明:方程有两个不相等的实数根.
(2)是否存在实数m,使方程的两个实数根互为相反数?若存在,求出m的值及两个实数根;若不存在,请说明理由
关于
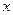 的方程为
的方程为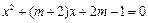 .
.(1)证明:方程有两个不相等的实数根.
(2)是否存在实数m,使方程的两个实数根互为相反数?若存在,求出m的值及两个实数根;若不存在,请说明理由
(1)证明略
(2)m的值为 - 2,方程的根为
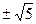
解(1)证明:△=(m+2)2-4(2m-1)=m2-4m+8=(m-2)2+4 ………2分
∵(m-2)2≥0 ∴(m-2)2+4>0
∴方程有两个不相等的实数根. ………3分
(2) 存在实数m,使方程的两个实数根互为相反数. ………4分
由题知:x1+x2=-(m+2)=0
解得:m =" -" 2 ………6分
将m =" -" 2代入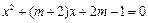 ,解得:x=
,解得:x=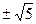
∴m的值为 - 2,方程的根为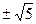 ………7分
………7分
∵(m-2)2≥0 ∴(m-2)2+4>0
∴方程有两个不相等的实数根. ………3分
(2) 存在实数m,使方程的两个实数根互为相反数. ………4分
由题知:x1+x2=-(m+2)=0
解得:m =" -" 2 ………6分
将m =" -" 2代入
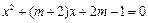 ,解得:x=
,解得:x=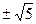
∴m的值为 - 2,方程的根为
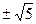 ………7分
………7分
练习册系列答案
相关题目
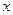 的一元二次方程
的一元二次方程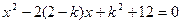 有实数根
有实数根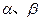 .
.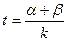 ,求t的最小值。
,求t的最小值。 2+b
2+b ;
;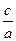 .
.
 的解是( )
的解是( )

 ,
,
 ,
,
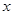 的方程
的方程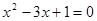 的根的情况是( )
的根的情况是( )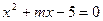 的一个根,求m的值及方程的另一根x2。
的一个根,求m的值及方程的另一根x2。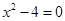 的解是 ( )
的解是 ( )



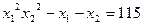 .
. (1) 求k的值;
(1) 求k的值;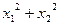 的值
的值