题目内容
关于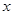 的方程
的方程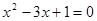 的根的情况是( )
的根的情况是( )
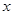 的方程
的方程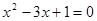 的根的情况是( )
的根的情况是( )| A.有两个不相等的实数根 | B.有两个相等的实数根 | C.没有实数根 | D.不能确定 |
A
方程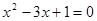 的根的判别式Δ=
的根的判别式Δ=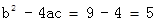 >0
>0
所以有两个不相等的实数根。
故选A
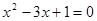 的根的判别式Δ=
的根的判别式Δ=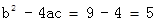 >0
>0所以有两个不相等的实数根。
故选A

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
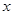 的方程
的方程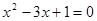 的根的情况是( )
的根的情况是( )| A.有两个不相等的实数根 | B.有两个相等的实数根 | C.没有实数根 | D.不能确定 |
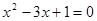 的根的判别式Δ=
的根的判别式Δ=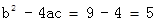 >0
>0
 名校课堂系列答案
名校课堂系列答案