Question

【题目】如图∠AOB＝120°，把三角板60°的角的顶点放在O处．转动三角板（其中OC边始终在∠AOB内部），OE始终平分∠AOD．

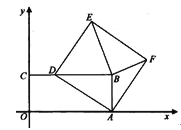
（1）（特殊发现）如图1，若OC边与OA边重合时，求出∠COE与∠BOD的度数．

（2）（类比探究）如图2，当三角板绕O点旋转的过程中（其中OC边始终在∠AOB内部），∠COE与∠BOD的度数比是否为定值？若为定值，请求出这个定值；若不为定值，请说明理由．

（3）（拓展延伸）如图3，在转动三角板的过程中（其中OC边始终在∠AOB内部），若OP平分∠COB，请画出图形，直接写出∠EOP的度数（无须证明）.

Answer 1

【答案】（1）∠BOD＝60°，∠COE＝30°；（2）∠COE：∠BOD＝；（3）画图见解析；∠POE＝30°．

【解析】

（1）∵OC边与OA边重合，如图1，根据角的和差和角平分线的定义即可得到结论；
（2）①0°≤∠AOC＜60°时，如图2，②当60°≤∠AOC≤120°时，如图3，根据角的和差和角平分线的定义即可得到结论；
（3）①0°≤∠AOC＜60°时，设∠AOC=α，∠BOD=β，②当60°≤∠AOC≤120°时，设∠AOC=α，∠BOD=β，根据角的和差和角平分线的定义即可得到结论．

（1）∵OC边与OA边重合，如图1，

∴∠AOD＝60°，∠BOD＝∠AOB﹣∠AOD＝120°﹣60°＝60°，

∵OE平分∠AOD，

∴∠COE＝AOD＝30°；

（2）①0°≤∠AOC＜60°时，如图2，

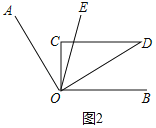
∵OE平分∠AOD，

∴∠DOE＝AOD，

∴∠COE＝∠COD﹣∠EOD＝60°﹣AOD，

∵∠DOB＝∠AOB﹣∠AOD＝120°﹣∠AOD，

∴∠COE：∠BOD＝；

②当60°≤∠AOC≤120°时，如图3，

∵OE平分∠AOD，

∴∠DOE＝AOD，

∴∠COE＝∠EOD﹣∠COD＝AOD﹣60°，

∵∠DOB＝∠AOD﹣∠AOB＝∠AOD﹣120°，

∴∠COE：∠BOD＝；

（3）①0°≤∠AOC＜60°时，

设∠AOC＝α，∠BOD＝β，

∵∠AOB＝120°，∠COD＝60°，

∴α+β＝60°，

∴∠AOD＝60°+α，∠BOC＝60°+β，

∵OE始终平分∠AOD，OP平分∠COB，

∴∠AOE＝AOD＝30°+ ，∠BOP＝BOC＝30°+，

∴∠POE＝∠AOB﹣∠AOE﹣∠BOP＝120°﹣（30°+）﹣（30°+）＝30°；

②当60°≤∠AOC≤120°时，

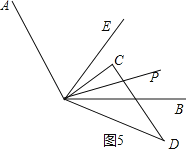
设∠AOC＝α，∠BOD＝β，

∵∠AOB＝120°，∠COD＝60°，

∴∠BOC＝120°﹣∠AOC＝60°﹣∠BOD，

∴120°﹣α＝60°﹣β，

∴α﹣β＝60°，

∴∠AOD＝120°+β，∠BOC＝60°﹣β，

∵OE始终平分∠AOD，OP平分∠COB，

∴∠DOE＝AOD＝60°+，∠BOP＝BOC＝30°﹣，

∴∠POE＝∠DOE﹣∠BOD﹣∠BOP＝（60°+）﹣β﹣（30°﹣）＝30°；

综上所述，∠POE＝30°．