题目内容
【题目】已知关于x的方程x2﹣(m+n+1)x+m(n≥0)的两个实数根为α、β,且α≤β.
(1)试用含α、β的代数式表示m和n;
(2)求证:α≤1≤β;
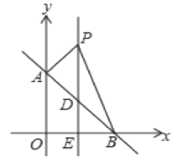
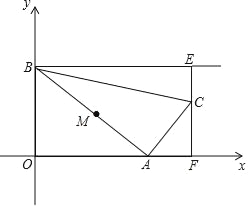
(3)若点P(α,β)在△ABC的三条边上运动,且△ABC顶点的坐标分别为A(1,2)、B(![]() ,1)、C(1,1),问是否存在点P,使m+n=
,1)、C(1,1),问是否存在点P,使m+n=![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)m=αβ,n=α+β﹣αβ﹣1;(2)详见解析;(3)详见解析.
【解析】分析:(1)、根据韦达定理即可得出答案;(2)、首先求出(1﹣α)(1﹣β)的值为-n,从而根据n的取值范围得出答案;(3)、先根据条件确定动点所在的边,然后再确定点的坐标.
详解:解:(1)∵α、β为方程x2﹣(m+n+1)x+m=0(n≥0)的两个实数根,
∴判别式△=(m+n+1)2﹣4n=(m+n﹣1)2+4n≥0,且α+β=m+n+1,αβ=m,
于是m=αβ,n=α+β﹣m﹣1=α+β﹣αβ﹣1;
(2)∵(1﹣α)(1﹣β)=1﹣(α+β)+αβ=﹣n≤0(n≥0),又α≤β,∴α≤1≤β;
(3)若使m+n成立,只需α+β=m+n+1=![]() ,
,
①当点M(α,β)在BC边上运动时,由B(![]() ,1),C(1,1),得
,1),C(1,1),得![]() ≤α≤1,β=1,
≤α≤1,β=1,
而α=![]() ﹣β=
﹣β=![]() ﹣1=
﹣1=![]() >1,故在BC边上存在满足条件的点,其坐标为(
>1,故在BC边上存在满足条件的点,其坐标为(![]() ,1)所以不符合题意舍去; 即在BC边上不存在满足条件的点
,1)所以不符合题意舍去; 即在BC边上不存在满足条件的点
②当点M(α,β)在AC边上运动时,由A(1,2),C(1,1),得α=1,1≤β≤2,
此时β=![]() ﹣α=
﹣α=![]() ﹣1=
﹣1=![]() ,又因为1<
,又因为1<![]() <2,故在AC边上存在满足条件的点,其坐标为(1,
<2,故在AC边上存在满足条件的点,其坐标为(1, ![]() );
);
③当点M(α,β)在AB边上运动时,由A(1,2),B(![]() ,1),得
,1),得![]() ≤α≤1,1≤β≤2,
≤α≤1,1≤β≤2,
由平面几何知识得, 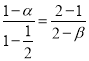 ,于是β=2α,由
,于是β=2α,由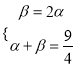 ,解得α=
,解得α=![]() ,β=
,β=![]() ,
,
又因为![]() <
<![]() <1,1<
<1,1<![]() <2,故在AB边上存在满足条件的点,其坐标为(
<2,故在AB边上存在满足条件的点,其坐标为(![]() ,
, ![]() ).
).
综上所述,当点M(α,β)在△ABC的三条边上运动时,存在点(1, ![]() )和点(
)和点(![]() ,
, ![]() ),使m+n=
),使m+n=![]() 成立.
成立.

【题目】为了加强公民的节水意识,合理利用水资源,我市采用价格调控的手段达到节水的目的,我市自来水收费的价目表如下表:
价目表 | |
每月用水量 | 单价 |
不超出6m3的部分 | 3元/m3 |
超出6m3不超出10m3的部分 | 5元/m3 |
超出10m3的部分 | 9元/m3 |
注:水费按月结算 | |
请根据如表的内容解答下列问题:
(1)填空:若该户居民2月份用水4m3,则应收水费_______元;
(2)若该户居民3月份用水am3(其中6m3<a<10m3),则应收水费多少元?(用含a的代数式表示,并化简)
(3)若该户居民4、5两个月共用水15m3(5月份用水量超过了4月份),设4月份用水xm3,求该户居民4、5两个月共交水费多少元?(用含x的代数式表示,并化简)