题目内容
【题目】如图,直线l1:y1=x和直线l2:y2=﹣2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.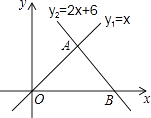
(1)求点A的坐标,并回答当x取何值时y1>y2?
(2)求△AOB的面积;
(3)当△POB的面积是△AOB的面积的一半时,求出这时点P的坐标.
【答案】
(1)解:∵直线l1与直线l2相交于点A,
∴y1=y2 , 即﹣2x+6=x,解得x=2,
∴y1=y2=2,
∴点A的坐标为(2,2);
观察图象可得,当x>2时,y1>y2
(2)解:由直线l2:y2=﹣2x+6可知,当y=0时,x=3,
∴B(3,0),
∴S△AOB= ![]() ×3×2=3
×3×2=3
(3)解:∵△POB的面积是△AOB的面积的一半,
∴P的纵坐标为1,
∵点P沿路线O→A→B运动,
∴P(1,1)或( ![]() ,1)
,1)
【解析】(1)将两个函数的解析式联立组成方程组,从而可求得点A的坐标,当y1>y2时,即y1的图像位置y2的上方,从而可求得x的值;
(2)令y2=0可求得求得B的横坐标,然后,根据三角形面积公式求解即可;
(3)根据三角形的面积公式可求得P的纵坐标,然后,将点B的纵坐标代入两直线解析式求得横坐标,即为符合题意的P点的坐标.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目