Question

【题目】如图，在中，，点分别在边上，沿所在的直线折叠，使点的对应点恰好落在边上，若和相似，则的长为______．

Answer 1

【答案】或

【解析】

先求出AC的长度，由△CEF与△ABC相似，分两种情况：①若CF：CE=3：4，此时EF∥AB，CD为AB边上的高；②若CE：CF=3：4，由相似三角形角之间的关系，可以推出∠B=∠ECD与∠A=∠FCD，从而得到CD=AD=BD，即D点为AB的中点．分别求出答案即可.

解：∵在中，，

∴，

若△CEF与△ABC相似，分两种情况：

①若CF：CE=3：4，

∵AC：BC=3：4，

∴CF：CE=AC：BC，

∴EF∥AB．

连接CD，如图1所示：

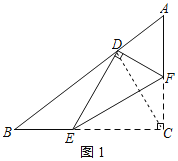
由折叠性质可知，CD⊥EF，

∴CD⊥AB，即此时CD为AB边上的高．

∵AB=5，

∴cosA=，

∴AD=ACcosA=3×，

∴BD=；

②若CE：CF=3：4，

∵AC：BC=3：4，∠C=∠C，

∴△CEF∽△CBA，

∴∠CEF=∠A．

连接CD，如图2所示：

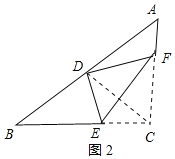
由折叠性质可知，∠CEF+∠ECD=90°，

又∵∠A+∠B=90°，

∴∠B=∠ECD，

∴BD=CD．

同理可得：∠A=∠FCD，AD=CD，

∴D点为AB的中点，

∴BD=；

故答案为：或．