题目内容
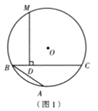
【题目】阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC>AB，M是
的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD=AB+BD．
下面是运用“截长法”证明CD=AB+BD的部分证明过程．
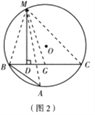
证明：如图2，在CB上截取CG=AB，连接MA，MB，MC和MG．
∵M是
的中点，
∴MA=MC
任务：（1）请按照上面的证明思路，写出该证明的剩余部分；
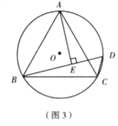
（2）填空：如图（3），已知等边△ABC内接于⊙O，AB=2，D为⊙O上 一点, 
，AE⊥BD与点E,则△BDC的周长是 ．
【答案】（1）证明见解析；（2）
．
【解析】试题分析: （1）首先证明△MBA≌△MGC（SAS），进而得出MB＝MG，再利用等腰三角形的性质得出BD＝GD，即可得出答案；
（2）方法一、首先证明△ABF≌ACD（SAS），进而得出AF＝AD，以及CD＋DE＝BE，进而求出DE的长即可得出答案．
方法二、先求出BE，再用（1）的结论得出BE＝CD＋DE，即可得出结论．
试题解析:
（1）证明：如图2，在CB上截取CG＝AB，连接MA，MB，MC和MG．
∵M是
的中点，
∴MA＝MC．
在△MBA和△MGC中
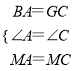
∴△MBA≌△MGC（SAS），
∴MB＝MG，
又∵MD⊥BC，
∴BD＝GD，
∴DC＝GC＋GD＝AB＋BD；
（2）解：方法一、如图3，截取BF＝CD，连接AF，AD，CD，
由题意可得：AB＝AC，∠ABF＝∠ACD，
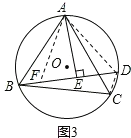
在△ABF和△ACD中
∵
，
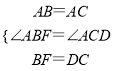∴△ABF≌ACD（SAS），
∴AF＝AD，
∵AE⊥BD，
∴FE＝DE，则CD＋DE＝BE，
∵∠ABD＝45°，
∴BE＝
，
则△BDC的周长是2＋2
．
故答案为：2＋2
．
方法二、∵△ABC是等边三角形，
∴BC＝AB＝2，∠ABC＝∠ACB，
∴由（1）的结论得，BE＝DE＋CD，
在Rt△ABD中，∠ABD＝45°，AB＝2，
∴BE＝
，
∴DE＋CD＝
，
∴则△BDC的周长是BC＋BD＋CD＝BC＋BE＋DE＋CD＝2＋2
．
故答案为：2＋2
．
点睛: 此题主要考查了全等三角形的判定与性质以及等腰三角形以及等边三角形的性质，正确作出辅助线利用全等三角形的判定与性质解题是解题关键．
