题目内容
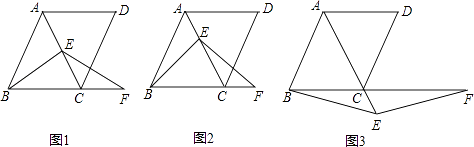
【题目】如图,在△ABC和△ADE中,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,OA、OC分别是∠PAC和∠PCA的角平分线.


(1)当∠APC =60°时,求∠AOC的度数;
(2)当AB⊥AC,AB=AD=4,AC=3,BC=5时,设AP=x,用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC,∠B=20°时,∠AOC的取值范围为α°<∠AOC <β°,直接写出α、β的值.
【答案】(1)∠AOC的度数为120°;(2)PD=![]() ,PD的最大值为
,PD的最大值为![]() ;(3)α=100,β=145.
;(3)α=100,β=145.
【解析】
(1)根据三角形内角和求得∠PAC+∠PCA的度数,然后根据角平分线的定义求得∠OAC+∠OCA的度数,从而求解;
(2)在△ABC中,当AP⊥BC时,AP最小,PD最大,由面积法求出AP的长,即可求出PD的最大值;
(3)如图,由已知可推出∠BAC=90°,设∠BAP=y,则∠PAC=90°-y,∠PCA=70°,
推出∠AOC=![]() y+100°,,因为0°<y<90°,可推出100°<∠AOC<145°,即可写出α、β的值.
y+100°,,因为0°<y<90°,可推出100°<∠AOC<145°,即可写出α、β的值.
解:在△APC中,∠PAC+∠PCA=180°-∠APC=120°
又∵OA、OC分别是∠PAC和∠PCA的角平分线
∴∠OAC+∠OCA=![]() ∠PAC+
∠PAC+![]() ∠PCA=
∠PCA=![]() (∠PAC+∠PCA)=60°
(∠PAC+∠PCA)=60°
∴在△OAC中,∠AOC=180°-60°=120°
(2)∵AD=AB=4,而PD=AD-AP=4-AP=4-x,
∴当AP⊥BC时,AP最小,PD最大,
此时,S△ABC=![]() BCAP=
BCAP=![]() ABAC,
ABAC,
即![]() ×5x=
×5x=![]() ×4×3,
×4×3,
解得,x=![]() ,
,
∴PD=![]() ,PD的最大值为:4-
,PD的最大值为:4-![]() =
=![]() ;
;
(3)如图,
![]()
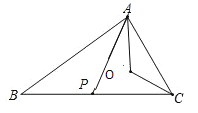
∵AB⊥AC,
∴∠BAC=90°,
设∠BAP=y,则∠PAC=90°-y,∠PCA=70°,
∵OA、OC分别是∠PAC和∠PCA的角平分线,
∴∠OAC=![]() ∠PAC,∠OCA=/span>
∠PAC,∠OCA=/span>![]() ∠PCA,
∠PCA,
∴∠AOC=180°-(∠OAC+∠OCA)
=180°-![]() (∠PAC+∠PCA)
(∠PAC+∠PCA)
=180°-![]() (90°-y+70°)
(90°-y+70°)
=![]() y+100°,
y+100°,
∵0°<y<90°,
∴100°<![]() y+100°<145°,
y+100°<145°,
即100°<∠AOC<145°,
∴α=100,β=145.

 阅读快车系列答案
阅读快车系列答案