题目内容
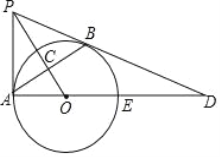
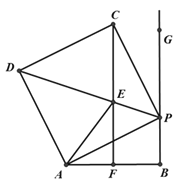
【题目】如图,线段AB=10,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP![]() △CEP;
△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长
【答案】(1)△AEP≌△CEP;(2)垂直 ; 理由见详解; (3)20 .
【解析】
(1)四边形APCD正方形,则DP平分∠APC,PC=PA,∠APD=∠CPD=45°,即可求解;(2)△AEP≌△CEP,则∠EAP=∠ECP,而∠EAP=∠BAP,则∠FCP+∠CMP=90°,则∠AMF+∠PAB=90°。(3)证明△PCN≌△APB(AAS),则CN=PB=BF,PN=AB,即可求解。
证明:(1)∵四边形APCD正方形,
∴DP平分∠APC, PC=PA,
∴∠APD=∠CPD=45°,
在△AEP和△CEP
PC=PA
∠APD=∠CPD
PE=PE
∴△AEP≌△CEP(SAS).
(2) CF⊥AB.
理由如下: ∵△AEP≌△CEP,
∴∠EAP=∠ECP,
∵∠EAP=∠BAP.
∴∠BAP=∠FCP,
∵∠FCP+∠CMP=90°,∠AMF=∠CMP,
∴∠AMF+∠PAB=90°,
∴∠AFM=90°,
∴CF⊥AB.
(3)过点 C 作CN⊥PB.可证得△PCN≌△APB,
∴ CN=PB=BF, PN=AB,
∵△AEP≌△CEP, ∴AE=CE,
∴AE+EF+AF
=CE+EF+AF
=BN+AF
=PN+PB+AF
=AB+CN+AF
=AB+BF+AF
=2 AB
=20.

练习册系列答案
相关题目