Question

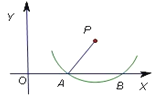
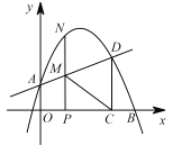
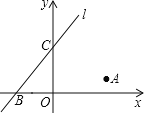
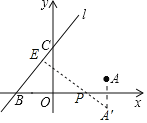
【题目】如图，在平面直角坐标系中，点A的坐标为（3，1），直线l与x轴，y轴分别交于点B（﹣3，0），C（0，3），当x轴上的动点P到直线l的距离PE与到点A的距离PA之和最小时，则点E的坐标是_____．

Answer 1

【答案】

【解析】

利用对称的性质找到A的对称点A'（3，﹣1），再利用直线l与直线A'E互相垂直，求出两条直线的解析式，最后联立方程即可求出交点E的坐标.

解：作点A关于x轴的对称点A'，过A'作A'D⊥l于E，与x轴交于点P，

则A'D即为所求最小值；

∵A的坐标为（3，1），

∴A'（3，﹣1），

∵B（﹣3，0），C（0，3），

直线BC所在的直线解析式y＝x+3，

∴A'E所在直线解析式y＝﹣x+2，

∴，

∴，

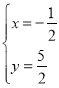∴E（﹣，），

故答案为（﹣，）；