题目内容
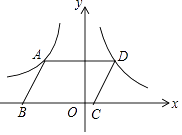
【题目】在矩形ABCD中,AB=6cm,BC=8cm,若将矩形对角线BD对折,使B点与D点重合,四边形EBFD是菱形吗?请说明理由,并求这个菱形的边长. 
【答案】解:四边形EBFD是菱形, 理由:∵将矩形对角线BD对折,使B点与D点重合,
∴EF垂直平分BD,
∴BO=DO,
∵四边形ABCD是矩形,
∴AD=BC,
∴∠EDB=∠DBC,
∴∠DEF=∠EFB,
在△EOD和△FOB中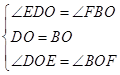 ,
,
∴△EOD≌△FOB(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形,
又∵BD⊥EF,
∴平行四边形BEDF是菱形;
设BE=x,
可得方程:62+(8﹣x)2=x2 ,
解得:x=6.25,
答:菱形的边长为6.25cm
【解析】首先利用翻折变换的性质得出BO=DO,进而得出∠DEF=∠EFB,求出△EOD≌△FOB,进而得出四边形BEDF是平行四边形,再利用BD⊥EF,得出平行四边形BEDF是菱形;利用菱形的性质以及勾股定理得出菱形的边长.
【考点精析】本题主要考查了菱形的判定方法和矩形的性质的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】如图,在△ABC中,D是AB中点,联结CD. 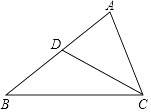
(1)若AB=10且∠ACD=∠B,求AC的长.
(2)过D点作BC的平行线交AC于点E,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,请用向量
,请用向量 ![]() 、
、 ![]() 表示
表示 ![]() 和
和 ![]() (直接写出结果)
(直接写出结果)