题目内容
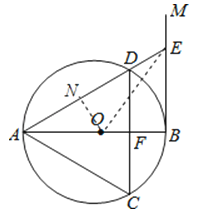
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且![]() =
=![]() ,连接AC,AD,延长AD交BM于点E.
,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
【答案】
(1)
证明:∵AB是⊙O的直径,BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BE,
∴CD⊥AB,
∴![]() =
=![]()
∵![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AD=AC=CD,
∴△ACD是等边三角形;
(2)
解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
∴∠DAC=60°
∵AD=AC,CD⊥AB,
∴∠DAB=30°,
∴BE=![]() AE,ON=
AE,ON=![]() AO,
AO,
设⊙O的半径为:r,
∴ON=![]() r,AN=DN=
r,AN=DN=![]() r,
r,
∴EN=2+![]() ,BE=
,BE=![]() AE=
AE=![]() ,
,
在Rt△NEO与Rt△BEO中,
OE2=ON2+NE2=OB2+BE2,
即(![]() )2+(2+
)2+(2+![]() )2=r2+
)2=r2+![]() ,
,
∴r=2![]() ,
,
∴OE2=![]() +25=28,
+25=28,
∴OE=2![]() .
.
【解析】(1)由AB是⊙O的直径,BM是⊙O的切线,得到AB⊥BE,由于CD∥BE,得到CD⊥AB,根据垂径定理得到![]() =
=![]() ,于是得到
,于是得到![]() =
=![]() =
=![]() ,问题即可得证;
,问题即可得证;
(2)连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,得到∠DAC=60°又直角三角形的性质得到BE=![]() AE,ON=
AE,ON=![]() AO,设⊙O的半径为:r则ON=
AO,设⊙O的半径为:r则ON=![]() r,AN=DN=
r,AN=DN=![]() r,由于得到EN=2+
r,由于得到EN=2+![]() ,BE=
,BE=![]() AE=
AE=![]() ,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
此题考查了圆的综合应用以及等边三角形的判定与性质和切线的性质以及勾股定理的应用.

 优加精卷系列答案
优加精卷系列答案【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 36 | 52 |
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?