题目内容
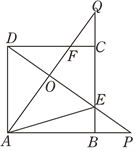
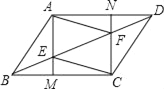
【题目】如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.
【答案】(1)证明见解析;(2)AB:AE=![]() :1.
:1.
【解析】(1)证明∵四边形ABCD是平行四边形(已知),
∴BC∥AD(平行四边形的对边相互平行)。
又∵AM丄BC(已知),∴AM⊥AD。
∵CN丄AD(已知),∴AM∥CN。∴AE∥CF。
又由平行得∠ADE=∠CBD,又AD=BC(平行四边形的对边相等)。
在△ADE和△CBF中, ∠DAE=∠BCF="90" ,AD=CB,∠ADE=∠FBC,
∴△ADE≌△CBF(ASA),∴AE=CF(全等三角形的对应边相等)。
∴四边形AECF为平行四边形(对边平行且相等的四边形是平行四边形)。
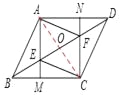
(2)如图,连接AC交BF于点0,当AECF为菱形时,则AC与EF互相垂直平分。
∵BO=OD(平行四边形的对角线相互平分),
∴AC与BD互相垂直平分。
∴![]() ABCD是菱形(对角线相互垂直平分的平行四边形是菱形)。
ABCD是菱形(对角线相互垂直平分的平行四边形是菱形)。
∴AB=BC(菱形的邻边相等)。
∵M是BC的中点,AM丄BC(已知),∴△ABM≌△CAM。
∴AB=AC(全等三角形的对应边相等)。∴△ABC为等边三角形。
∴∠ABC=60°,∠CBD=30°。
在Rt△BCF中,CF:BC=tan∠CBF=![]() 。
。
又∵AE=CF,AB=BC,∴AB:AE=![]() 。
。
(1)根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE∥CF;然后由ASA推知△ADE≌△CBF;最后根据全等三角形的对应边相等知AE=CF,根据对边平行且相等的四边形是平行四边形的判定得出结论。
(2)如图,连接AC交BF于点0.由菱形的判定定理推知平行四边形ABCD是菱形,根据菱形的邻边相等知AB=BC;然后结合已知条件“M是BC的中点,AM丄BC”证得△ADE≌△CBF(ASA),所以AE=CF(全等三角形的对应边相等),从而证得△ABC是正三角形;最后在Rt△BCF中,利用锐角三角函数的定义求得CF:BC=tan∠CBF=![]() ,利用等量代换知(AE=CF,AB=BC)AB:AE=
,利用等量代换知(AE=CF,AB=BC)AB:AE=![]() 。
。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共![]() 只,这两种节能灯的进价、售价如下表:
只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 |
|
|
乙型 |
|
|
(1)如何进货,进货款恰好为![]() 元?
元?
(2)设商场购进甲种节能灯![]() 只,求出商场销售完节能灯时总利润
只,求出商场销售完节能灯时总利润![]() 与购进甲种节能灯
与购进甲种节能灯![]() 之间的函数关系式;
之间的函数关系式;
(3)如何进货,商场销售完节能灯时获利最多且不超过进货价的![]() ,此时利润为多少元?
,此时利润为多少元?