题目内容
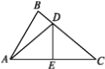
【题目】如图,在Rt△ABC中,∠BAC=90°,且BA=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为_______.

【答案】![]()
【解析】
由勾股定理求出BC的长,再证明四边形DEAF是矩形,可得EF=AD,根据垂线段最短和三角形面积即可解决问题.
解:∵∠BAC=90°,且BA=9,AC=12,
∴在Rt△ABC中,利用勾股定理得:BC=![]() =
=![]() =15,
=15,
∵DE⊥AB,DF⊥AC,∠BAC=90°
∴∠DEA=∠DFA=∠BAC=90°,
∴四边形DEAF是矩形,
∴EF=AD,GF=![]() EF
EF
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=![]() AB×AC=
AB×AC=![]() BC×AD,
BC×AD,
∴AD=![]() =
=![]() =
=![]() ,
,
∴EF=AD=![]() ,因此EF的最小值为
,因此EF的最小值为![]() ;
;
又∵GF=![]() EF
EF
∴GF=![]() ×
×![]() =
=![]()
故线段GF的最小值为:![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】泸西某著名风景旅游景点于5 月1日前后相继开放,为了更好的吸引游客前去游览,某景点给出团体购买公园门票票价如下:
购票人数 | 1~50 | 51~100 | 100人以上 |
每人门票(元) | 13元 | 11元 | 9元 |
今有甲、乙两个旅行团,已知甲团人数少于50人,乙团人数不超过100人.若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计应付门票费1080元.
(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?