题目内容
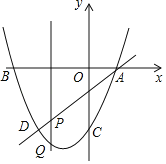
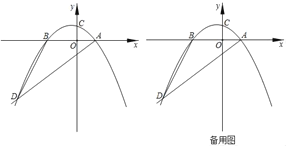
【题目】如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( )

A.①③④B.①②④C.②③④D.①②③④
【答案】B
【解析】
①由非负数的性质,即可证得y2=﹣(x﹣2)2﹣1≤﹣1<0,即可得无论x取何值,y2总是负数;
②由抛物线l1:y1=a(x+1)2+2与l2:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),可求得a的值,然后由抛物线的平移的性质,即可得l2可由l1向右平移3个单位,再向下平移3个单位得到;
③由 y1﹣y2=﹣(x+1)2+2﹣[﹣(x﹣2)2﹣1]=﹣6x+6,可得随着x的增大,y1﹣y2的值减小;
④首先求得点A,C,D,E的坐标,即可证得AF=CF=DF=EF,又由AC⊥DE,即可证得四边形AECD为正方形.
解:①∵(x﹣2)2≥0,
∴﹣(x﹣2)2≤0,
∴y2=﹣(x﹣2)2﹣1≤﹣1<0,
∴无论x取何值,y2总是负数;
故①正确;
②∵抛物线G:y1=a(x+1)2+2与抛物线H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),
∴当x=1时,y=﹣2,
即﹣2=a(1+1)2+2,
解得:a=﹣1;
∴y1=﹣(x+1)2+2,
∴H可由G向右平移3个单位,再向下平移3个单位得到;
故②正确;
③∵y1﹣y2=﹣(x+1)2+2﹣[﹣(x﹣2)2﹣1]=﹣6x+6,
∴随着x的增大,y1﹣y2的值减小;
故③错误;
④设AC与DE交于点F,
∵当y=﹣2时,﹣(x+1)2+2=﹣2,
解得:x=﹣3或x=1,
∴点A(﹣3,﹣2),
当y=﹣2时,﹣(x﹣2)2﹣1=﹣2,
解得:x=3或x=1,
∴点C(3,﹣2),
∴AF=CF=3,AC=6,
当x=0时,y1=1,y2=﹣5,
∴DE=6,DF=EF=3,
∴四边形AECD为平行四边形,
∴AC=DE,
∴四边形AECD为矩形,
∵AC⊥DE,
∴四边形AECD为正方形.
故④正确.
故选:B.