题目内容
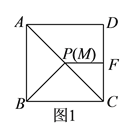
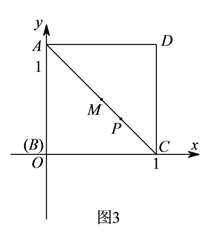
【题目】有这样一个问题:探究函数![]() 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(![]() )函数
)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.
中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.

(![]() )结合函数的图象,写出该函数的一条性质:__________.
)结合函数的图象,写出该函数的一条性质:__________.
【答案】(![]() )任意实数(
)任意实数(![]() )见解析(
)见解析(![]() )当
)当![]() 时,
时,![]() 随
随![]() 增大而增大
增大而增大
【解析】试题分析:
(1)由![]() 可知
可知![]() 可取任意实数;
可取任意实数;
(2)根据表格中的数据描点、连线画出图形即可;
(3)本题答案不唯一,只要符合图象所反映的实际情况都可以.
试题解析:
(![]() )
)![]() 取值范围是全体实数.
取值范围是全体实数.
(![]() )根据表格中所提供的数据,描点、连线,画出该函数的图象如下图所示:
)根据表格中所提供的数据,描点、连线,画出该函数的图象如下图所示:
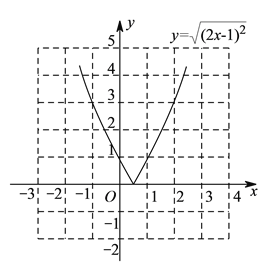
(![]() )由图可得:当
)由图可得:当![]() 时,
时,![]() 随
随![]() 增大而增大(答案不唯一).
增大而增大(答案不唯一).

练习册系列答案
相关题目
【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批 粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的 粒数m | 96 | 282 | 382 | 570 | 948 | 1912 | 2850 |
发芽的 频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.956 | 0.950 |
则绿豆发芽的概率估计值是( )
A. 0.96 B. 0.95 C. 0.94 D. 0.90