题目内容
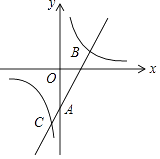
【题目】如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为 
，点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为（ ）
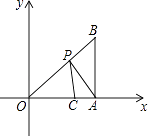
A.
B.
C.2
D.
【答案】B
【解析】解：作A关于OB的对称点D，连接CD交OB于P，连接AP，则此时PA+PC的值最小，
∵DP=PA，
∴PA+PC=PD+PC=CD，
∵B 
，
∴AB= 
，OA= ，
∵∠OAB=90°，
∴∠B=∠AOB=45°，
由勾股定理得：OB=AD=2，
∵C（1，0），
∴CD= 
，
即PA+PC的最小值是
故选B．
作A关于OB的对称点D，连接CD交OB于P，连接AP，则此时PA+PC的值最小，根据勾股定理求出CD，即可得出答案．
练习册系列答案
阅读快车系列答案
相关题目
【题目】用A4纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元．在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元．
设在同一家复印店一次复印文件的页数为x(x为非负整数)．
(1)根据题意，填写下表：
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 |
| 2 |
| … |
乙复印店收费(元) | 0.6 |
| 2.4 |
| … |
(2)设在甲复印店复印收费y1元，在乙复印店复印收费y2元，分别写出y1，y2关于x的函数关系式；
(3)当x＞70时，顾客在哪家复印店复印花费少？请说明理由．
