Question

【题目】如图，一艘船在A处望见灯塔E在北偏东60°方向上，此船沿正东方向航行60海里后到达B处，在B处测得灯塔E在北偏东15°方向上．

（1）求∠AEB的度数；

（2）①求A处到灯塔E的距离AE；

②已知灯塔E周围40海里内有暗礁，问：此船继续向东方向航行，有无触礁危险？（参考数据：≈1.414，≈1.732）

Answer 1

【答案】（Ⅰ）45°；（Ⅱ）此船继续向正东方向航行，无触礁危险．

【解析】

（1）根据方向角的概念、三角形内角和定理计算即可；

（2）作BM⊥AE，EH⊥AB，求出AM、BM，得到AE，根据正弦的概念求出EH，比较即可得到答案．

（Ⅰ）∠AEB=180°﹣30°﹣90°﹣15°=45°；

（Ⅱ）①作BM⊥AE，EH⊥AB，垂足分别为M，H，

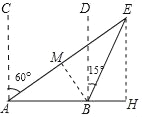
∵AB=60，∠MAB=30°，

∴BM=30，AM=ABcos∠MAB=60×cos30°=30，

∵∠MBE=90°﹣∠AEB=90°﹣45°=45°=∠AEB，

∴EM=ME=30，

∴AE=30+30≈82（海里），

∴EH=15+15≈41（海里），

②EH=41＞40，

∴此船继续向正东方向航行，无触礁危险．