题目内容
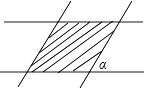
【题目】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断AC与DF的位置关系,并说明理由;
(2)若∠C比∠A大20°,求∠F的度数.

【答案】(1)AC∥DF,理由见解析;(2)40°.
【解析】
(1)根据平行线的性质得出∠ABD=∠C,求出∠D=∠ABD,根据平行线的判定得出AC∥DF;
(2)根据平行线的性质和三角形内角和解答即可;
解:(1)AC∥DF,理由如下:
∵∠1=80°,∠2=100°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠ABD=∠C,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF;
(2)∵AC∥DF,
∴∠A=∠F,∠ABD=∠D,
∵∠C=∠D,∠1=80°,
∴∠A+∠ABD=180°﹣80°=100°,
即∠A+∠C=100°,
∵∠C比∠A大20°,
∴∠A=40°,
∴∠F=40°.

练习册系列答案
相关题目
【题目】某集团购买了150吨物资打算运往某地支援,现有甲、乙、丙三种车型供选择,每辆汽车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 1000 | 1200 | 1500 |
(1)若全部物资都用甲、乙两种车型来运送,需运费24000元,问分别需甲、乙两种车型各多少辆?
(2)若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送,请你写出可能的运送方案,并帮助该集团找出运费最省的方案(甲、乙、丙三种车辆均要参与运送).