题目内容
【题目】如图，在Rt△AOB中，∠AOB=90°，AO=
，BO=1，AB的垂直平分线交AB于点E，交射线BO于点F．点P从点A出发沿射线AO以每秒
个单位的速度运动，同时点Q从点O出发沿OB方向以每秒1个单位的速度运动，当点Q到达点B时，点P、Q同时停止运动．设运动的时间为t秒．
（1）当t= 时，PQ∥EF；
（2）若P、Q关于点O的对称点分别为P′、Q′，当线段P′Q′与线段EF有公共点时，t的取值范围是 .
【答案】
；
【解析】解：（1）如图1，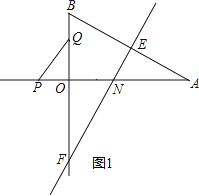
当PQ∥EF时，则∠QPO=∠ENA，
又∵∠AEN=∠QOP=90°，
∴△AEN∽△QOP，
∵∠AOB=90°，AO=
，BO=1，
∴tanA=
=
=
，
∴∠A=∠PQO=30°，
∴
==
，
解得：t=
，
故当t=时，PQ∥EF；
所以答案是：；
（2）如图2，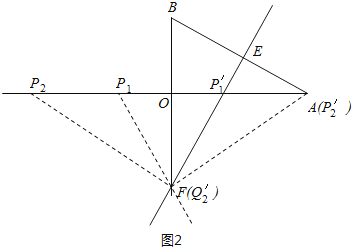
当P点介于P1和P2之间的区域时，P1′点介于P1′和P2′之间，此时线段P′Q′与线段EF有交点，
当P运动到P1时，
∵AE=
AB=1，且易知△AEP1′∽△AOB，
∴
，∴AP1′=
，
∴P1O=P1′O=，
∴AP1=AO+P1O=
，
∴此时P点运动的时间t=
=
s，
当P点运动到P2时，
∵∠BAO=30°，∠BOA=90°，
∴∠B=60°，
∵AB的垂直平分线交AB于点E，
∴FB=FA，
∴△FBA是等边三角形，
∴当PO=OA=时，此时Q2′与F重合，A与P2′重合，
∴PA=2，则t=1秒时，线段P′Q′与线段EF有公共点，
故当t的取值范围是：≤t≤1 ．
所以答案是：≤t≤1 ．
【考点精析】本题主要考查了平行线的性质和线段垂直平分线的性质的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题．
