题目内容
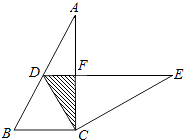
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
求证:(1)![]()
(2)![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)只要证明△BDF≌△ADC,推出BD=AD,推出∠BAD=∠ABD=2∠CBE=2∠DAC即可解决问题.
(2)延长BE、DG交于点K.先证明Rt△AEF≌Rt△KEG,再根据其性质即可得到结论.
证明:(1)∵AD⊥BC,
∴∠ADC=90°
∵AB=BC,E为AC中点,
∴∠ABE=∠CBE=![]() ∠ABC,BE⊥AC,
∠ABC,BE⊥AC,
∴∠BEC=90°,
∴180°-∠C-∠ADC=180°-∠C-∠BEC
即∠CBE=∠CAD,
在△BDF和△ADC中, ,
,
∴△BDF≌△ADC(AAS),
∴BD=AD,
∴∠BAD=∠ABD=2∠CBE=2∠DAC.
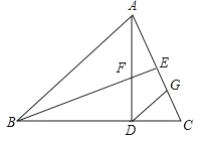
(2)延长BE、DG交于点K.
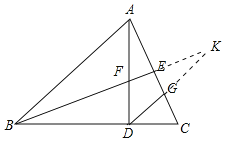
∵DG∥AB,
∴∠CGD=∠CAB,∠K=∠ABE,
∵∠BAC=∠C,
∴∠CGD=∠C
∵∠K=∠CBE=∠CAD
∠AEF=∠KEG=90°,∠EAF=∠EKG,
∴DG=DC,DK=BD,
∴DG=DF,DK=BD=AD,
∴DK-DG=AD-DF,即GK=AF
在Rt△AEF和Rt△KEG中
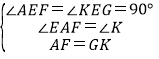 ,
,
∴Rt△AEF≌Rt△KEG (AAS),
∴EF=EG.

 寒假学与练系列答案
寒假学与练系列答案【题目】在下图的直角坐标系中,将△ABC平移后得到△A’B’C’,它们的个顶点坐标如下表所示
△ABC | A(0,0) | B(3,0) | C(5,5) |
△A'B'C' | A'(4,2) | B'(7,b) | C'(c,d) |
(1)观察表中各对应点坐标的变化,并填空:△ABC向______平移______个单位长度,再向______平移______个单位长度可以得到△A'B'C';
(2)在坐标系中画出△ABC及平移后的△A'B'C';
(3)求出△A'B'C'的面积.