题目内容
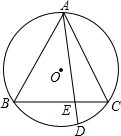 如图,⊙O是△ABC的外接圆,且AB=AC,弦AD交BC于点E,AE=4,ED=2,求AB的长.
如图,⊙O是△ABC的外接圆,且AB=AC,弦AD交BC于点E,AE=4,ED=2,求AB的长.
分析:连接BD构造相似三角形△ABE∽△ADB,然后根据相似三角形的对应边成比例求得AB2=AD•AE,从而求得AB的长度.
解答: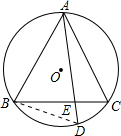 解:连接BD,如图,AB=AC,
解:连接BD,如图,AB=AC,
则
=
,
∴∠ABE=∠D(等弧所对的圆周角相等),(3分)
又∠BAE=∠BAD(公共角),
∴△ABE∽△ADB(AA),
∴
=
(相似三角形的对应边成比例),(6分)
∴AB2=AD•AE,又AE=4,ED=2,得AD=6,(7分)
∴AB=2
. (9分)
 解:连接BD,如图,AB=AC,
解:连接BD,如图,AB=AC,则
 |
| AB |
 |
| AC |
∴∠ABE=∠D(等弧所对的圆周角相等),(3分)
又∠BAE=∠BAD(公共角),
∴△ABE∽△ADB(AA),
∴
| AB |
| AD |
| AE |
| AB |
∴AB2=AD•AE,又AE=4,ED=2,得AD=6,(7分)
∴AB=2
| 6 |
点评:本题综合考查了相似三角形的判定与性质、圆周角定理.圆心角与它所对的弧、所对的弦之间的关系:这三个量中,若有一个量相等,则其它的量两个量也相等.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
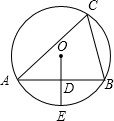 如图,⊙O是△ABC的外接圆,OD⊥AB于点D、交⊙O于点E,∠C=60°,如果⊙O的半径为2,那么OD=
如图,⊙O是△ABC的外接圆,OD⊥AB于点D、交⊙O于点E,∠C=60°,如果⊙O的半径为2,那么OD= 24、如图,AD是△ABC的高,且AD平分∠BAC,请指出∠B与∠C的关系,并说明理由.
24、如图,AD是△ABC的高,且AD平分∠BAC,请指出∠B与∠C的关系,并说明理由. (2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( )
(2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( ) (2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
(2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.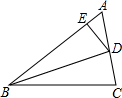 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.